Построение графика функции и присвоение ей значения в каждой точке. Предел функции. Исследование функции на непрерывность, страница 3

1.104 > 1, следовательно, ряд расходится.

7.  Найти указанные интегралы.

а)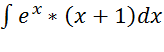

Поскольку интеграл неопределенный, воспользуемся кнопкой «символьного расчета» (→).

б)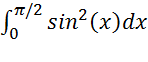

Интеграл определенный. Воспользуемся «вычислительным равно» (=).

в)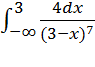

8. Найти 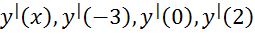, если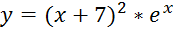

Для нахождения  воспользуемся функцией «Производная» на панели «Исчисление»:

Для того, чтобы найти значение производной в точке -3, надо присвоить переменной х значение -3 и повторить операцию. Таким же образом найдем значение производной при всех остальных значениях х:

9. Найти обратную для матрицы .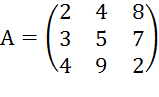

Присвоим матрицу для А:

Для нахождения обратной матрицы для матрицы А воспользуемся кнопкой «Инверсия» на панели инструментов «Матрица». Установим в маркер значение, для которого надо найти обратную матрицу и введем «вычислительное равно» (=):

ВТОРОЙ УРОВЕНЬ

Найти контурные токи, решив систему уравнений электрического состояния цепи.

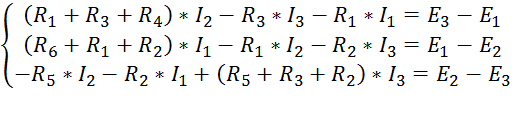
где:

Присвоим каждому показателю заданное значение:

Сведем данную систему в матрицу А, учитывая индексацию силы тока , а ответы в вектор-столбец свободных членов В:

Для нахождения результатов воспользуемся оператором lsolve:

Разложить в ряд Макларена функцию 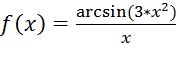. Проверить результат графически.

Для разложения функции в ряд Макларена можно воспользоваться оператором «_series,_», находящуюся на панели символьных ключевых слов. В левый маркер оператора копируем функцию, которую надо разложить, а после запятой можно указать степень, до которой нужно разложить ряд:

Для графической проверки присвоим f(x), f1(x), f10(x) полученные значения соответственно и отобразим их на графике, как это делалось ранее:

Вычислить определенный интеграл с точностью ξ = 0,0001

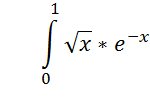
Для нахождения определенного интеграла воспользуемся знаком «вычислительное равно» (=).

Для задания степени точности результата следует выполнить следующую операцию: Выделить результат, затем «Формат→Результат» и в открывшемся окне на вкладке «Формат чисел» установить требуемое число знаков после запятой.

При дальнейшем разложении данной функции в ряд Макларена и нахождения интегралов по результатам разложения определили, что расхождения начинаются после седьмого знака после запятой.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Дан набор точек. Заранее определим требуемые нам значения для дальнейшей работы и построим график.

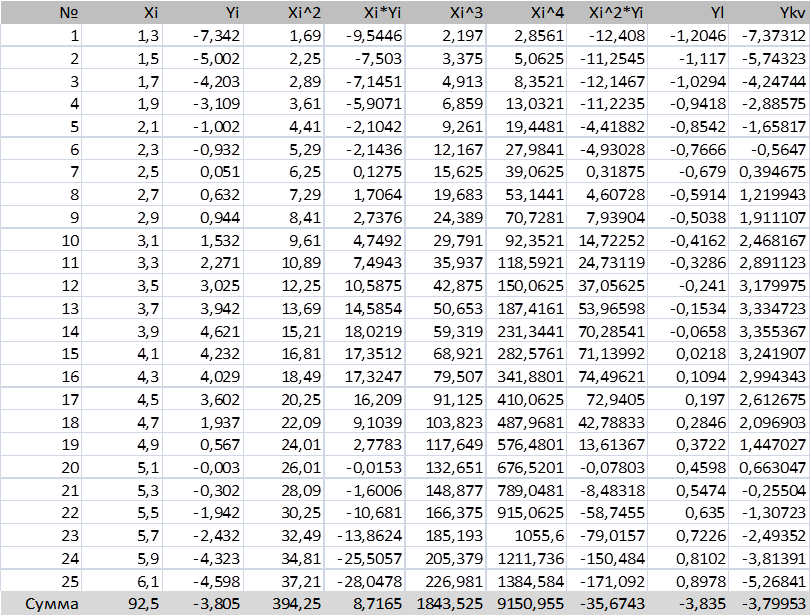Где:

Yl – определенная функция линейной зависимости;

Ysq – определенная функция квадратичной зависимости.

График по точкам Х и У.

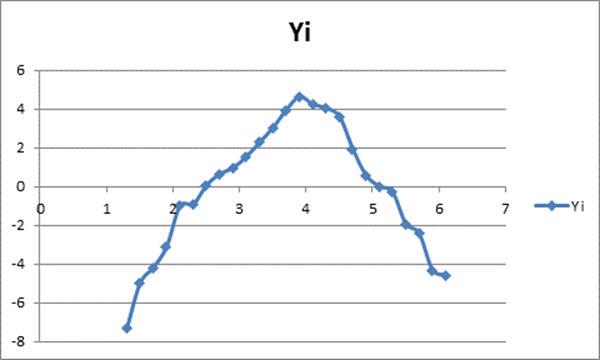
Определим тип зависимости. Это может быть линейная зависимость и квадратичная.

1. Тип линейной зависимости: у = a*x + b. Для определения линейной зависимости сведем полученные ранее значения в систему уравнений:

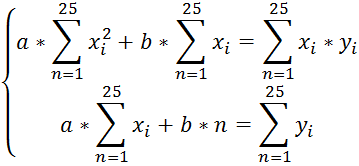
Получим:

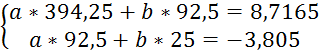
Решим данную систему:

Получим решение:

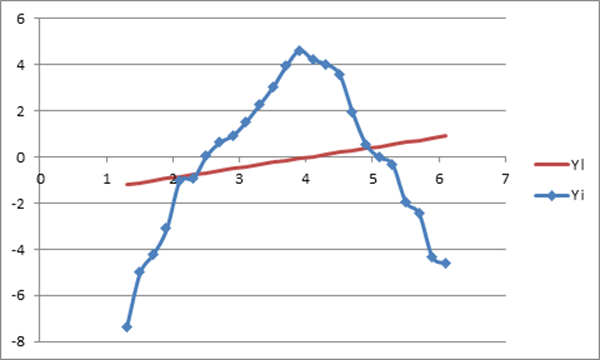
Таким образом, определи коэффициенты a и b для линейной зависимости. Данная зависимость будет иметь вид:

y = 0,438*x – 1,774.

Подставив данное уравнение к уже имеющимся значениям, получим координаты точек. Построим график:

2. Тип квадратичной зависимости: . Для определения квадратичной зависимости сведем полученные ранее значения в систему уравнений:

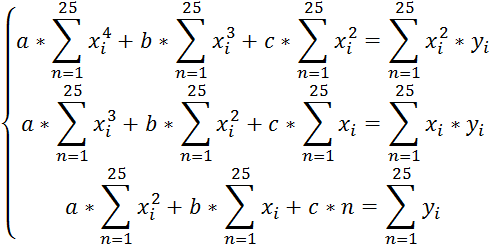
Получим:

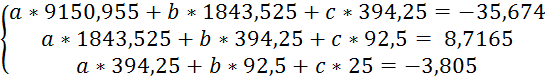
Решим данную систему:

Получим решение:

Таким образом, определили коэффициенты a, b и c для квадратичной зависимости. Данная зависимость будет иметь вид:

y = -1.676*x² + 12.841*x – 21.236

Подставив данное уравнение к уже имеющимся значениям, получим координаты точек. Построим график:

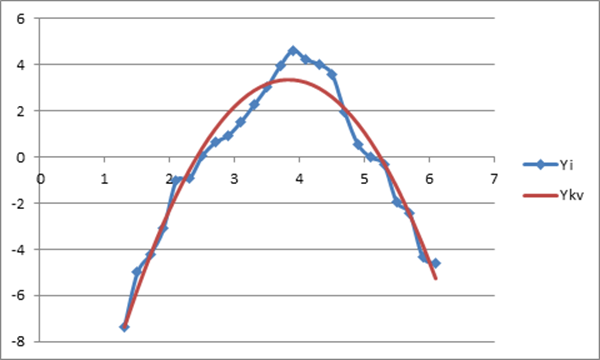
Таким образом, определили, что уравнение y = -1.429*x² + 10.328*x – 16.75 лучше всего описывает кривую, построенную на первом графике (по заданным точкам).