Построение графика функции и присвоение ей значения в каждой точке. Предел функции. Исследование функции на непрерывность, страница 2

Построим графики функций для каждого уравнения. Для этого выразим  и  из уравнений. Присвоим полученные значения у1(х) и у2(х) соответственно:

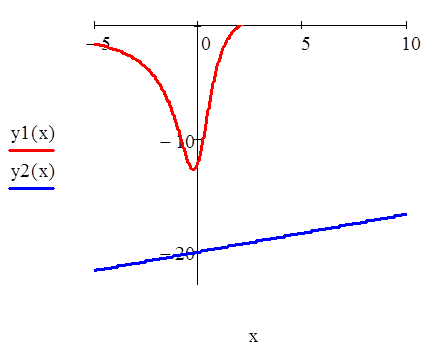
На панели инструментов «График» вызываем график в декартовой системе координат. В маркер горизонтальной оси задаем значение переменной х, а вертикальной оси, имя функции у1(х) и у2(х) через запятую, а также диапазон значений по осям. Поскольку данные графики не пересекаются, система решения не имеет. Об этом также будет свидетельствовать выделенный красным оператор Find.

4.  Найти предел функции. Результаты проверить графически.

а)  и при х→∞, х→10, х→-10;

Присвоим аргументу предела значение функции у(х):

Вызовем график в декартовой системе координат. В горизонтальной оси зададим значения по х, а в вертикальной у(х). А также, зададим диапазон значений по осям:

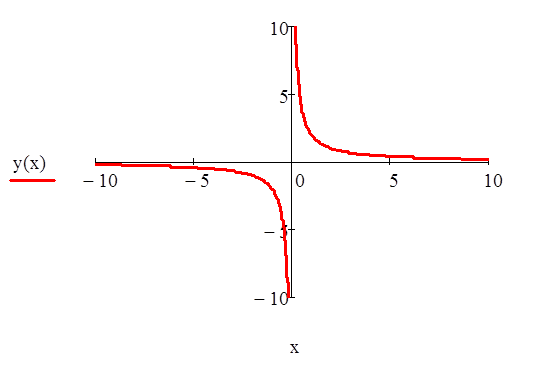
Найдем значение предела справа и слева:

Полученные значения означают, что предел функции   при х→0 стремится к ∞.

Найдем значения пределов функций при других х:

Поскольку не возникает трудностей при нахождении значения предела, нет необходимости находить значения пределов слева и справа.

б)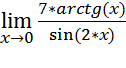

Чтобы найти значение предела при х→0, воспользуемся знаком «символьного расчета» (→). Поскольку не возникает трудностей с нахождением значения, находить значения пределов слева и справа нет необходимости:

Для графической проверки присвоим функции у(х) аргумент предела. На панели «График» выберем график в декартовой системе координат. На горизонтальной оси зададим значение х, а вертикальной – у(х), а также диапазон значений по осям. Вызвав окно редактирования графика, включим маркеры и в маркер по оси y копируем полученное ранее значение:

в)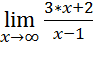

Чтобы найти значение предела при х→∞, воспользуемся знаком «символьного расчета» (→). Поскольку не возникает трудностей с нахождением значения, находить значения пределов слева и справа нет необходимости:

Для графической проверки присвоим функции у(х) аргумент предела. На панели «График» выберем график в декартовой системе координат. На горизонтальной оси зададим значение х, а вертикальной – у(х), а также диапазон значений по осям. Вызвав окно редактирования графика, включим маркеры и в маркер по оси y копируем полученное ранее значение:

5.  Исследовать функцию на непрерывность.

а)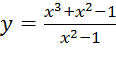

Для нахождения разрыва функции построим ее график. График функции строится аналогично предыдущим, описанным в задании.

Видно, что функция разрывна в точка при х→1 и х→-1.

Для определения рода разрыва найдем значения пределов данной функции в каждой точке при подходе слева и справа:

На основе полученных значений можно сделать вывод, что в точках при х→1 и х→-1 разрыв второго рода.

б)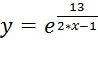

Выполним операции, аналогичные описанным в пункте «а» данного задания:

График показывает, что функция разрывна в точке при х→. Определим род разрыва. Для этого найдем значения пределов функции слева и справа:

На основании полученных значений можно сделать вывод, что в точке при х→ разрыв второго рода.

6.  Исследовать ряд на сходимость двумя способами.

а)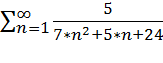

Для исследования ряда введем некоторое значение S.

S= → …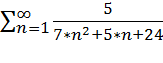

Если S - ∞, то ряд расходится. Если S – число, то ряд сходится. Если S неопределенно, то ряд расходится.

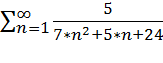→0,441

Можно сделать вывод, что ряд сходится.

Проверим указанный вывод по радикальному признаку Каши. По виду общего члена ряда составляется функция путем замены п на х:

А затем находим интеграл общего члена ряда с переменой х. Если интеграл равен числу, то ряд сходится, если не равен числу, ряд расходится.

Ряд сходится.

б)

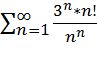
Поскольку невозможно определить значение для данного ряда, то воспользуемся признаком Даламбера.

Р =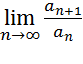

Если Р < 1, то ряд сходится;

Если Р > 1, то ряд расходится.