Неопределенный интеграл. Интегрирование степенных функций. Интегрирование по частям. Интегрирование рациональных дробей

Министерство путей сообщения Российской Федерации

Дальневосточный государственный университет путей сообщения

Кафедра «Высшая математика»

Н.С.  

ВЫСШАЯ МАТЕМАТИКА

Методические указания по выполнению контрольных работ № 3, 4 для студентов ИИФО всех специальностей, обучающихся по ускоренной программе (на базе техникума)

Хабаровск

Издательство ДВГУПС 2002

УДК 51(075.8)

ББК В 1 я73

     К 650

Рецензент:

Кандидат физико-математических наук, доцент кафедры «Высшая математика» Дальневосточного 

государственного университет путей сообщения

              

К 650    Высшая математика: Методические указания по выполнению контрольных работ № 3, 4 для студентов ИИФО всех специальностей, обучающихся по ускоренной программе (на базе техникума). – Хабаровск: Изд-во ДВГУПС, 2002. – 34 с.: ил.

Методические указания содержат варианты заданий (индивидуальных) контрольных работ № 3, 4 по основным разделам курса. Каждое задание сопровождается решением подобного примера. 

Предназначены для студентов ИИФО всех специальностей, обучающихся по ускоренной программе (на базе техникума).

УДК 51(075.8)

ББК В 1 я73

 Издательство  Дальневосточного государственного     университета путей сообщения (ДВГУПС), 2002

ВВЕДЕНИЕ

Методические указания по выполнению контрольных работ составлены для студентов всех специальностей Института интегрированных форм обучения (ИИФО), занимающихся по ускоренной программе (на базе техникума).

Задания контрольных работ № 3–4 включают основные разделы курса «Высшей математики»: неопределенный и определенный интегралы, вычисление площади плоской фигуры, однородные и неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, числовые и степенные ряды, приложения степенных рядов. Студенту предлагается выполнить 12 заданий (8 – в контрольной работе № 3; 4 – в контрольной работе № 4) и ответить на теоретические вопросы.

Каждое задание сопровождается решением подобного примера, что позволит студенту самостоятельно выполнить индивидуальное задание.

КОНТРОЛЬНАЯ РАБОТА № 3

Методические указания и задания

РАЗДЕЛ 1. Неопределенный интеграл

Рассмотрим правила интегрирования неопределенных простейших интегралов. Кратко смысл задания сводится к следующему.

При помощи преобразований привести интеграл к табличному, затем, используя таблицу интегралов, найти первообразную:

                                                                                             ∫ f ( x )dx = F( x )+C , где f ( x ) – подынтегральная функция; F( x ) – первообразная; C – произвольная постоянная.

Таблица основных интегралов дана ниже, где «a » и «b» – постоянные коэффициенты, причем a ≠ 0, а «b» – любое.

Таблица интегралов

1. (ax +b )n dx = 1 ( ax + b )n+1 + C;	1`.  xndx = xn+1 +C,n ≠ 1;

∫∫

                                                      a       n +1                                          n +1

                       dx        1                                                      dx

2. ∫       =      ln ax + b + C;     2`.  ∫ = ln + C; ax + b      a x

3. ∫ sin(ax +b)dx = − ¹ cos(ax + b)+ C;     3`.  ∫sinxdx = −cos(x)+C; a

4. 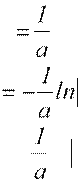∫cos(ax + b)dx    sin(ax + b)+ C;   4`.  ∫cosxdx = sinx +C;

5. ∫tg(ax + b)dxcosax + b+ C; 5`.  ∫tgxdx = −ln cosx + C;

6. ∫ctg(ax + b)dx = ln sin(ax + b)+ C; 6`.  ∫ctgxdx = ln sinx + C;

7. ∫axdx = ax + C; lna	7`.  ∫eαxdx = ex +C; α
dx 8. ∫ x2 + a2 = a1 arctg ax + C;	dx 8`.  ∫ x2 +1 = arctgx + C;
dx 9.                    = arcsin x + C;	dx                   9`.                    = arcsinx+C;

∫∫

                       a2 − x2                    a                                        1− x²

10. ∫     2dx− a2 = 2¹aln x^x +^−aa +C;        10`.  ∫ x₂dx−1 = ¹2ln ^xx +⁻¹1+C;

x

                                 dx             1                                               dx

11. ∫     2(ax + b) = a tg(ax + b)+ C; 11`.  ∫ cos2x = tgx + C; cos

12. ∫     ₂(dxax + b ) = − a¹ ctg(ax + b )+ C. 12`.  ∫ sin^dx₂ x = −ctgx + C.

sin

1.1. Интегрирование степенных функций

Наиболее распространенным является интеграл от степенной функции (таблица интегралов, с. 4). Для вычисления этих интегралов необходимо знать следующие правила действий со степенями:

xm      m−n ;   xm xn = xm+n ;   n xm = x mn , = x xn

где m,n – любое.

Учитывая эти правила, рассмотрим вычисление интеграла от степенной функции:

∫₈^{3 2} − 5x +^dx = x

                                                                3           3         

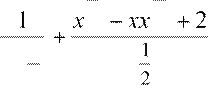
                      = ∫^{3 2} − 5x +   1          ^{4           4}     dx =

_x

8

                                                3x 4                 x           

                                                     −1         3                                         

= ∫ x2 − 5x + x ₄ + x 4−12 − x1+13−12 + 2x−12 dx = 3

                                  8                    3                                              

                                                                                              

                                                                                              

                                                                               −¹+1         ¹+1         ⁷+1            −¹+1

                                3 x3               x2 1 x 4                x 4          x 6               x 2

                          =        − 5      +   ⋅           +         −         + 2            + C =

                                 8 3                 2 3 − 1 +1 1 +1 7 +1              − 1 +1

                                                                                4           4           6                 2

                      = x3 − 5 x2 + 4 x 34 + 4 x 54 − 6 x136 + 4x 12 + C =           

                                     8 2            9          5          13

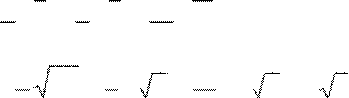= 1 x3 − 5 x2 + 4 4 x3 − 4 x4 x − 6 x2 6 x + 4 x + C.

                                8          2          9             5            13

Задание

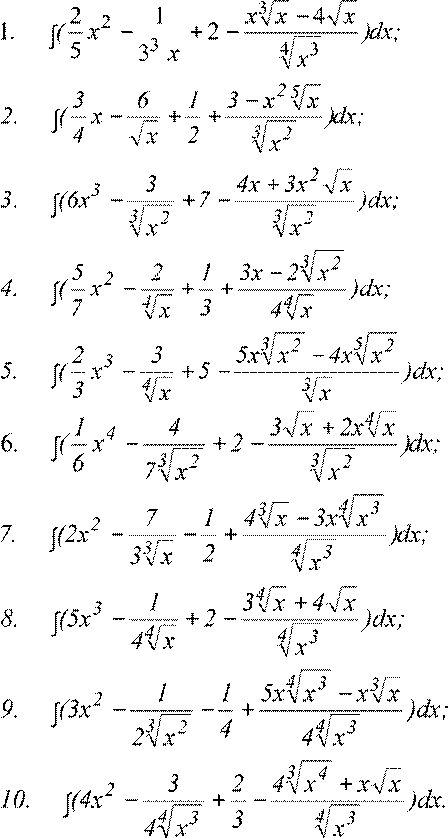
Примечание. 1, 2, 3 и т.д. – номер варианта.

1.2. Интегрирование заменой переменной

Этот метод интегрирования основан на введении в подынтегральную функцию новой переменной величины и ее дифференциала, причем замену переменной необходимо подбирать таким образом, чтобы в исходном интеграле присутствовал дифференциал новой переменной в явном виде. Рассмотрим несколько примеров.

Пример 1

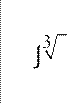
                                                                  cos( x ) +1 = t                                  1            

∫ ³ cos( x +1) sinxdx = dt = −sin(x )dx =    t(−dt ) = −∫t ³dt = ^t+ C = sin xdx = −dt          

=  ³ (cos x +1)⁴ + C.

Пример 2

= arctgt + C = arctge

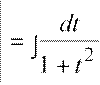
                      ∫                           ^ex2x dx =^ex =⁼e^txdx^x + C.

1+ edt

Пример 3

ln x = t

                                                 dx                           ^dt

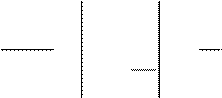                                          ∫         =       dx = ∫    = lnt + C = lnln x + C.

                                              xln x     dt =           t

x

Замечание. После введения новой переменной и вычисления интеграла необходимо вернуться к исходной переменной.

Задание 

5.  a ) ∫ arctg1 32x dx;     б ) ∫ x2tgx3dx;

                                      + x                                                          e_x

                                        6.xdx;                                       б ) ^∫    2_x dx;

1+ e

7.  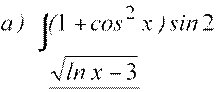а ⁾∫   dx;     б ⁾ ∫ x³⁵ 5x⁴ +1dx;

x

8.  а )∫ e²xe^x dx;                          б ) ^∫ _xdx2 +1 dx;              

cos

x

                          ∫ arcsin³ x                                      б ) ∫( x³ + 4)¹⁰ x²dx;

9.  а )          dx;

1− x²

10.  а )∫ ln2 x − 5ln xdx;        б ) ∫ 4 x4 + 4x( x3 +1)dx.

x

1.3. Интегрирование по частям

Формула интегрирования по частям имеет вид∫UdV =U ⋅V − ∫VdU , т.е. исходный интеграл ∫ f ( x )dx мы должны, введя новые функции U и V , представить в виде ∫UdV , а затем построить правую часть формулы. По такой формуле вычисляются интегралы вида: ∫ xⁿ sin xdx; ∫ xⁿe^xdx;

∫ xⁿ cos xdx; причем вместо x может быть линейная подстановка (ax + b).

В этом случае степенная функция xⁿ обозначается функцией U ,  а dV – все остальные множители. Причем формулу интегрирования по частям можно применять многократно, например, в вышеуказанных интегралах формулу необходимо применить «n» раз.

Пример 1

x =U;dx = dU

∫ xcos2xdx = cos2xdx = dV                                .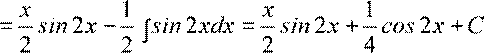

V 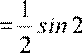x

Кроме указанных интегралов по этой же формуле вычисляются интегралы вида: ∫lnxdx; ∫arctgxdx;∫arcsinxdx и т.п.

Пример 2

arctgx = U; dU =^xdx

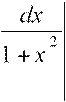∫ arctgxdx =                                 = xarctgx − ∫^{1+ x}₂ =

dV = dx; V = x

1+ x² = t;

= xarctgx − dt = 2xdx; −  = xarctgx − ¹ lnt + C = xarctgx − ¹ ln1+ x² + C.

                                                                                                             2                                  2

xdx  dt

Пример 3

                                                                 ln5x = U; dU = ^dx ;                        xdx

∫ln5xdx = x = xln5x − ∫  = dx = dV; x = V^x

= xln5x − ∫ dx = xln5x − x + C.

Задание 

1.  ∫ 2xcos3x + ln xdx;

2.  ∫(5x −1)sin2x + arctgxdx;

3.  ∫(1− x )e^3x + ln3xdx;

4.  ∫( x + 3)sin ^x + arcsinxdx;

2

5.  ∫( x − 2)e^−2xdx + ln( x +1)dx;

6.  ∫( x +1)cos4x + arctg ^x dx;

7. 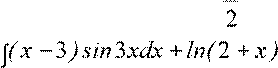 dx;

8.  ∫(4 − x )e^−xdx + arctg(2x +1)dx;

9.  ∫(2x − 3)cos ^x + arcsin2xdx;

2

10.  ∫(1− 3x )e^4x + ln( x + 4)dx.      

1.4. Интегрирование рациональных дробей

Рациональной дробью называется выражение вида 

Qm( x )

,

Rn( x )

где Qm( x ) и Rn( x) – рациональные многочлены степени m и n.

Если m ≥ n, то дробь называется неправильной, если m < n , то дробь