Расчет показателей обогащения при идеальном разделении. Фракционный состав углей и флюоритовых руд, страница 14

,%	,%	,%
4 22  60	65 80  85	2,88  5,99  9,11	104,2  98,0  91,8	67,8  78,40  78,0

Итак, максимум I соответствует  =22%, т.е. оптимальную границу следует провести таким образом, чтобы по одну сторону находились фракции с содержанием выше, чем  22%,  - хвостовая часть, а по другую - с содержанием ниже 22 % - концентратная часть. В табл.4, 5 границы проведены жирной линией.

Пример 3. Метод подбора концентратных фракций. Данный метод также позволяет определить оптимальную границу разделения при любом количестве физических свойств, используемых для сепарации. Данный метод более ориентирован на машинный расчет.

Суть метода заключается в следующем. Выбирают одну самую богатую фракцию (очевидно, что для угля эта фракция с максимальным содержанием золы) и ее принимают за концентрат. Для нее вычисляют ,,  и проводят границу разделения (см. пример I). Далее к этой фракции присоединяют вторую фракцию с ближайшим большим (для угля - меньшим) содержанием полезного компонента. Для составленного из этих фракций концентрата точно так же вычисляют , , и проводят границу.

Действия повторяются, пока критерий оптимальностинедостигнет максимума.

Для примера возьмем те же исходные данные (табл. 4) и ту функцию цен (23). Пример расчета приведен в табл.15.

Таблица 15

Выбор оптимальной границы разделения методом перебора

концентратных фракций

Содержание золы в самой "бедной" фракции, %
2,5 3,0 3,8 19,0 20,0 59,0	2,5 2,7 2,88 4,65 5,99 9,11	30 50 83 73 80 85	105 104,6 104,2 100,7 98,0 91,8	31,5 82,3 87,8 73,5 78,4 78,0

Таким образом, максимальный критерий оптимальности получается тогда, когда содержание в последней (самой зольной) фракции концентрата равно 20 %, Это значит, что границу разделения надо провести таким образом, чтобы в концентрат входили все фракции с содержанием 20 % и меньше (это уголь), а в хвосты - с содержанием 20 % и больше. В табл.4,5  граница показана жирной линией.

Варианты заданий

Для вариантов 1-10 - табл.1 и табл.6.

;

Для вариантов 11-16 - табл.2 и табл.7.

;

Для вариантов 17-29 - табл.3 и табл.8.

Работа 7. ВЫЧИСЛЕНИЕ СЕПАРАЦИОННЫХ ХАРАКТЕРИСТИК ТЕХНОЛОГИЧЕСКИХ СХЕМ

Задание. Вычислить сепарационные характеристики для указанных в варианте продуктов и схемы.

Вычисление сепарационной характеристики. Для обогатительных аппаратов сепарационная характеристика обычно далека от идеальной ступенчатой. Именно поэтому аппараты объединяются в технологические схемы таким образом, чтобы результирующая сепарационная характеристика схемы e_рез(x) была близка к идеальной.

В соответствии с общим подходом, результирующей сепарационной характеристикой (двухпродуктовой) схемы назовём отношение масс (производительностей) элементарной фракции в концентрате q_к и в исходном питании q_исх:

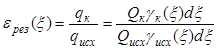,        (25)

Сепарационная характеристика для любого промежуточного продукта аналогично равна отношению производительностей (масс) узкой фракции в  i-ом продукте и в питании схемы:

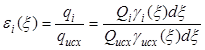,      (26)

Сепарационные характеристики для любых продуктов находят решением системы линейных уравнений. Число таких уравнений равно удвоенному числу операций в cxеме. Для любой i-ой операции имеем уравнения. Первое – сумма входящих потоков узкой фракции равна сумме выходящих:

,            (27)

второе – поток фракции в концентрате равен потоку её в питании, умноженному на сепарационную характеристику:

,            (28)