Расчет показателей обогащения при идеальном разделении. Фракционный состав углей и флюоритовых руд, страница 10

Формула (17) обобщает уравнение Белоглазова (16) для смеси частиц с 0 <k < k_max. Задача состоит в нахождениичисленных значений g(k₁),g(к₂),…,g(k_n) по экспериментальным ординатам e_тв(0), e_тв(Dt), e_тв(2Dt)... взятым в дискретные моменты времени t=0, Dt, 2Dt,.. . Для ее решения по формуле (17) нужно составить систему уравнений.

Определение b(k)  нуждается в дополнительной экспериментальной кривой кинетики извлечения интересующего ценного металла e_Ме(t)  и в сравнении ее с соответствующим теоретическим выражением:

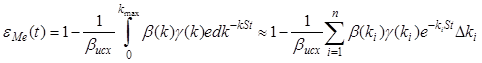,(18)

где b(k_i) - неизвестное содержание ценного компонента в i-й флотофракции частиц с k=k_i, %;  b_исх - известное среднее содержание в исходной смеси, b_исх=const.

Записывая равенство (18) для дискретных моментов времени t=0, Dt, 2Dt,… получим систему уравнений с n неизвестными ординатами b₁=b(k₁), b₂=b(k₂),…, b_n=b(k_n) искомой функции b(k). Решение системы дает функцию b(k).

Чтобы найти b(k) для другого ценного металла, нужна экспериментальная кривая e_Ме(t) по данному металлу.

Пример флотометрического анализа. Проба апатитовой руды флотировалась а лабораторной машине в следующих конкретных условиях: крупность 50 % - 200 меш; = 12,5% P₂O₅; =2,8% Р₂О₅; реагенты NaОH –75 г/т; жидкое стекло - 50 г/т; собиратель - 40 г/т. Экспериментальныекинетические кривые e_хв(t) и e_Ме(t)  имеют следующий вид:

Вначале рассчитаем степень аэрации в машине:

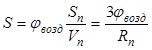,      (19)

где j_возд – объёмная доля воздуха в машине; S_п , V_п и R_п - площадь поверхности, объем и радиус "среднего "пузырька воздуха.

Если j_возд =0,1; R_п=0.0015 м,  то S_п = (3×0,1):0,0015=200 м²/м³.

Теперь определим диапазон флотируемости 0<k<k_max. Приближённо можно считать, что флотируемая часть руды (32 %) имеет среднюю флотируемостьk_ср=k_max/2 тогда с учётом формулы (16) экспериментальную кривую кинетики можно представить в виде

…(20)

Подставив координаты какой-либо экспериментальнойточки, вычислим k_max. Например, для t=1 мин имеем:

0,17=0,68(1- е^-100kmax). Усреднив k_max по нескольким экспери-ментальным точкам, получим k_max=0,7×10^-2 м/мин. В каждом варианте k_max задается индивидуально.

Диапазон флотируемости 0- k_max разобьемна триинтервала размером   Dk=0,24×10^-2 м/мин; значения искомой g(k) надо вычислить в дискретных точках на серединах интервалов, т.е. при k₁=0,12×10^-2 м/мин, k₂=0,36×10^-2 м/мин, k₃=0,6×10^-2 м/мин

Перепишем уравнения (17) и (18) следующим образом:

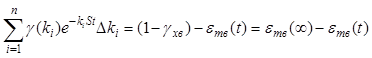,    (21)

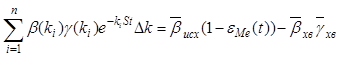.        (22)

Обозначим  g₁=g(0,12×10^-2); g₂=g(0,36×10^-2);  g₃=g(0,6×10^-2) и  развернем уравнение (21) и систему алгебраических линейных уравнений для моментов времени  t=0 мин; t=0,5 мин; t=1,0 мин:

0,24×10^-2(g₁+g₂+g₃)=1-0,68;

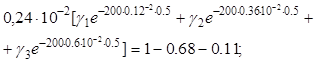
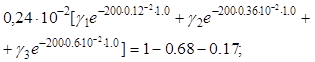
Решение этой системы уравнений: g₁=18,54 мин/м; g₂=52,45 мин/м; g₃=62,33 мин/м;

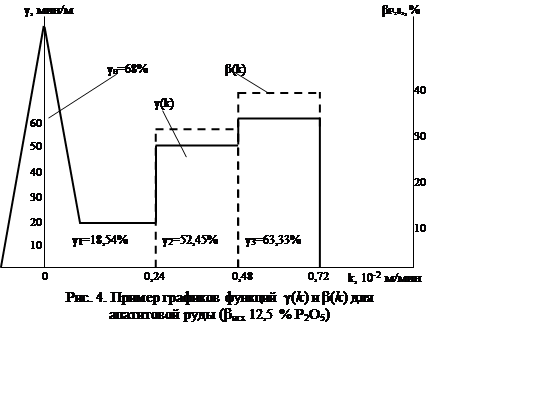
g₁Dk=0,0445; g₂Dk =0,1259; g₃Dk =0,1496. График найденной g-функции показан на рис. 4.

Аналогично, используя равенство (22), составим систему уравнений для определения значений искомой функции b(k) в дискретных точках  b₁=b(0,12×10-2), b₂=b(0,36×10-2), b₃=b(0,6×10-2) при t, равном соответственно 0; 0,5; 1,0 мин:

0,0445b₁+ 0,1259b₂+ 0,1496b₃=12,5(1-0)-0,68×2,8;

0,0445×0,89b₁+0,I259×0,7b₂ 0,1496×0,55b₃=12,5(1-0,32)-0,68×2,8;

0,0445×0,78b₁+0,1259×0,48b₂+0,1496×0,3b₃=12,5(1-0,52)-0,68×2,8.