Расчет показателей обогащения при идеальном разделении. Фракционный состав углей и флюоритовых руд, страница 13

Задание. По заданному фракционному составу исходного сырья вычислить оптимальную границу разделения:

а) для простейшего "одномерного" случая (табл.1-3);

б) для "двумерного" случая (табл.6-8) методом варьирования бортовых содержаний;

а) для "двухмерного" случая методом перебора концентратных фракций.

Вычисление оптимальной границы разделения. Выбор оптимальной границы разведения - важная задача, от решения которой зависят потери сырья, эксплуатационные и капитальные расходы и т.д.

Рассмотрим выбор оптимальной границы разделения на примерах.

Пример I. Простейший случай - одно физическое свойство, один извлекаемый компонент  в сырье. Функция b(x) меняется монотонно. Фракционный состав сырья приведен  работе 1. Задан также критерий оптимальности, например, экономически равный сумме максимальной прибыли, полученной с единицы массы сырья:

,     (23)

где Q_исх производительность по исходному, т/ч;   - соответственно выход и содержание расчетного компонента в концентрате;  -  функция цен, т.е. заданная зависимость цены за. 1 т концентрата от содержания в нем расчетного компонента .

Задача расчета - вычистить координату границы разде-ления,    дающую максимум критерия I. Оптимальное, значение вычисляется из уравнения

 .                (24)

Допустим, функция цены в условных денежных единицах за тонну задана выражением (24):

Перебираем все возможные варианты границы разделения и для каждого варианта вычисляемg_к и b_к , f_ц и величину I. Результаты вычислений сведем в табл. 13.

Таблица 13

Результаты вычисления

Таким образом, оптимальная плотность разделения для данного случая составляла около 1,8 г/см³.

Точно границу разделения можно получить либо построив график зависимости I отr_р , либо, если есть аналитические выражения функций g и b , по формуле (23).

Выход расчетного компонента в концентрат определяется просто суммированием; - как 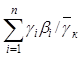например, для плотности разделения 1,5 г/см³.

для плотности 1,6 г/см³

и т.д.

Пример 2. Использование нескольких физических свойств. При комбинированном обогащении граница становится не точкой, а линией (для двух физических свойств), поверхностью (для трех физических свойств) и т.д. Следовательно приходится исследовать на экстремум функционалы   I , зависящие от искомых функций j_р(x₁, x₂,…, x_n). B этом случае используется метод "варьирования бортовых содержаний", пригодный дня любого типа схем и сырья.

Рассмотрим нахождение оптимальной границы разделения для случая комбинирования двух методов обогащения при двухпродуктовой сепарации. Задан фракционный состав (табл.4) и, например, экономический критерий оптимальности вида (23). Требуется найти положения оптимальной двухмерной границы разделения  максимизирующие критерий I . Решение производится по стадиям. Сначала намечаются несколько варьируемых (бортовых) содержаний и для каждого проводится своя линия разделения  таким образом, чтобы по одну сторону этой линии находились фракции с содержанием, большим ,а по другую - с меньшим. Затем для каждой границы вычисляютсяи  по формулам (3), (5), затем вычисляются и . При каком-то значении получим максимум значения I, следовательно, это значение и будет оптимальной границей разделения.

Результаты вычислений приведены в табл.14. значения , т.е. такие же, как в примере 1.

Таблица 14

Нахождение оптимальной границы разделения