Определение закона движения многозвенной системы

Для кинематического и силового анализа необходимо знать законы движения начальных звеньев, т.е. изменение обобщённых координат  от времени. Динамическое исследование машины основаны на решении второй задачи динамики – по заданным силам определить движение.

Механизм машины обычно состоит из нескольких звеньев. Определение закона движения многозвенной системы представляет сложную задачу, для решения которой следует составить уравнения движения механизма. Число этих уравнений равно числу степеней свободы механизма. Уравнения могут быть заданны в различных формах. Для механизмов с одной степенью свободы, основной составления уравнения движения является теорема об изменении кинетической энергии:

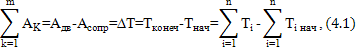
где  –  кинетическая энергия механизма в конце и в начале рассматриваемого промежутке времени,  – кинетическая энергия звена  в конце и начале рассматриваемого промежутка времени, A_k – работа каждой из внешних и внутренних сил, действующих на звенья механизма за этот промежуток времени, n – число подвижных звеньев, m –число сил.

Решение такого уравнения требует значительного объёма вычислений. Для механизмов с  W=1 (одной степенью свободы) возможно всю многозвенную кинематическую цепь заменить динамической моделью (одним условным звеном), которое движется так, что обобщённая координата совпадает в любой момент времени с обобщённой координатой механизма. Таким образом, в любой момент времени для начального звена будет справедливо уравнение (4.2)

в котором  – условная скорость начального звена, – условная скорость модели.

Если начальное звено совершает вращательное движение (рис 4.1а), то уравнение (4.1) можно заменить тождественным ему уравнением движения вращающегося звена (рис 4.1б), называемого звеном приведения. Момент инерции этого звена

J^пр назовём приведённым моментом инерции. Полученная расчётная схема называется одномассовой динамической моделью механизма.