Определение закона движения многозвенной системы, страница 2

Для звена приведения

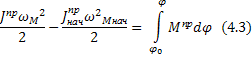
По условию  должна совпадать с угловой скоростью начального звена; .

Чтобы уравнения (4.1) и (4.2) были тождественными необходимо и достаточно, выполнение равенств

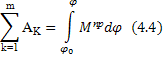
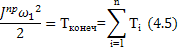
Если для любого момента времени выполняется соотношение (4.5), то удовлетворяется выражение

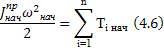
Из (4.4) можно найти , а из (4.5) .

Таким образом, при построении модели механизма все силы и моменты, действующие на него звенья, должны быть приведены к одному звену, называемого приведённым, и заменены приведённым моментом (или приведённой силой). Аналогично массы всех звеньев приводят к одному звену и заменяют суммарным приведённым моментом инерции, который эквивалентен всей инертности механизма. В итоге рассматриваемый многозвенный механизм, нагруженный сложной системой сил и моментов, заменяется моделью, состоящей из одного приведённого звена. Подчеркнём, что динамическая модель должна быть  настроена так, чтобы было выполнено уравнение (4.2). В противном случае сам переход от реального механизма к его модели теряет смысл.

как следует из уравнения Лангранжа II рода, при приведении сил должно соблюдаться равенство элементарных работ, и при приведении масс – равенство кинетических энергии.

Приведение сил и моментов сил. Приведённым моментом сил M^пр  называется момент пары сил, условно приложенный к звену приведения и определяемой из равенства работы этой пары: сумме элементарных работ и пар сил, действующих на звенья механизма.

При стационарных геометрических связях равенство элементарных работ одновренменно означает равенство их мощьностей.

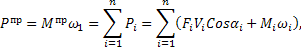
следовательно:

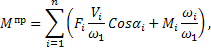
Аналогично при приведении к силе имеем