Общая характеристика проблемы социально­психологического обеспечения процесса подготовки воинских коллективов, страница 4

в) ход решения задачи в любой момент времени оценивается по состоянию системы знаний СПО. Несоответствие реального состояния требуемому определяет внутреннюю активность системы СПО и вызывает направленную перестройку процесса обработки информации.

Таким образом, повышение оперативности, достоверности сбора и обработки социально-психологической информации и обоснованности принимаемых решений возможно путем оптимизации структуры и состава автоматизированной системы сбора и анализа социально-психологической информации (АСАСПИ) о состояниях дежурных смен частей РКО.

1.3. Пути оптимизации структуры и состава автоматизированных систем сбора и анализа социально-психологической информации о состояниях воинских коллективов

Задача оптимизации структуры и состава вычислительных систем (ВС) формулируется в работах [3,  34] следующим образом. При заданных объемно-временных характеристиках информацион­ных потоков, параметрах технических средств и зависимостях пока­зателей их функционирования и стоимости от производительности определить такую структуру и состав системы, при которой приведенные затраты на создание и эксплуатацию данной системы мини­мальны, а показатели качества обслуживания удовлетворяют задан­ным требованиям пользователей.

Критерий оптимизации - минималь­ные приведенные затраты на создание и эксплуатацию ВС - является аддитивным относительно технических устройств и каналов связи, входящих в состав системы.

Качество ВС определяется в первую очередь временем пребыва­ния задач в системе.  Обозначим быстродействия устройств, входя­щих в состав АСАСПИ,  как V, а трудоемкость решаемых задач как Q. Тогда средняя длительность обслуживания  задачи  u=Q/V,  а  интенсивность решения задачи m=1/u. Время пребывания задачи в устройстве i,  согласно [25] будет

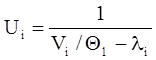                   (1.1)

Как указывается в работах [3, 25] выражение (1.1) справед­ливо для случая, когда предметом синтеза являются устройства, быстродействие которых может быть плавно изменено. Однако во многих случаях приходится ориентироваться на устройства, имеющи­еся в распоряжении пользователей. Технические параметры этих устройств фиксированы, а потребность системы в определенных ре­сурсах производительности должна удовлетворяться за счет выбора необходимого числа устройств, рекомендуемых к применению. Если исходить из равномерности загрузки устройств внутри каждой груп­пы, то время пребывания задачи внутри каждой i-й группы уст­ройств системы будет

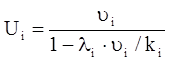;                  (1.2)

где к_i- количество однотипных устройств в i-й  группе  элементов системы.

В процессе решения одной задачи происходит в среднем a_i об­ращений к устройству i. Величины коэффициентов передач a_i и ин­тенсивностей потоков обращений к i-му элементу системы определя­ются из решения системы уравнений:

l×(P-J)=0,

где l=½½l_i: ½½ – матрица-строка интенсивностей обращения к i-му устройству, ; l_i=a_i×l_o; P - матрица вероятностей пе­редач заявок между элементами системы обработки информации.

С учетом выражения (1.2) среднее время обработки социаль­но-психологической информации для одного оператора в системе, состоящей из n элементов, составит

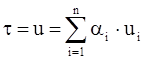                  (1.3)

Значение u существенно зависит от быстродейс­твия и количества устройств, входящих в состав АСАСПИ. В свою очередь быстродействие V_i есть функция стоимости устройства S_i. Предположим, что в пределах допустимых вариаций эта зависимость линейна, т.е. S_i=k_i×V_i, где k_i - коэффициент пропорциональности, отражающий стоимость единицы быстродействия устройства типа i. В таком случае стоимость системы распределяется на n составляющих

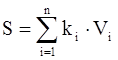                (1.4) 

Учитывая выражения (1.3) и (1.4), в формальной постановке задачи синтеза системы сбора и анализа социально-психологической информации могут быть представлены следующим образом [3]:

1. Задача минимизации времени обработки информации при фик­сированном уровне стоимостных затрат. При этом:

t = U(K_j,V_i,Q_i,l_i) ® min            (1.5)

при условии

S(k_i,к_j,V_i,S_i) £ S_o;

2. Задача минимизации стоимости системы при условии, что время решения задачи не превысит заданный уровень. При этом:

S(k_i,к_j,V_i) ® min              (1.6)

при условии

u(к_j,V_i,Q_i,l_i) £ u^*.

Параметр u^* определяет время реакции системы на запрос о результатах решения задачи оператором. Величина этого параметра имеет верхний предел, определяемый необходимостью соблюдения психологических условий диалога ЭВМ с человеком. Из [3] следу­ет, что параметр u^* не должен превышать величины 30 сек, т.е. u£30 сек.

В рассмотренной выше постановке задачи вида (1.5) и (1.6) решены Клейнроком [23]. Кроме этого, анализ их решения подробно при­водится в [25]. Результаты решения указанных двух типов задач синтеза системы приведены в табл.1.2.

Задача вида (1.5) соответствует случаю, когда уровни всех видов затрат и номенклатура средств, отпускаемых на организацию социально-психологического обеспечения, фиксированы.

Наиболее часто на практике возникает задача второго типа. Именно в этой форме решение задачи позволяет наиболее рационально подобрать параметры элементов системы, отвечающие конкретным условиям ее функционирования.

Таблица 1.2.

Тип задачи	Рациональные значения производительности устройств системы
1
2

В работах [8, 18, 24, 25, 28] изложены методы синтеза вычислительных систем. Сравнительная характеристика изложенных методов предс­тавлена в табл.1.3.

Результаты, полученные на основе применения рассмотренных методов, позволяют приближенно оценивать характеристики исследуе­мых систем, выбирать их конфигурации или, как минимум, отсеивать неудачные варианты, определять области значений параметров уст­ройств, в которых значение критерия эффективности экстремально.