4. Вынужденные колебания вагона без трения в подвешивании.
4.1. Получение общего решения
При выборе расчетной схемы используем следующие допущения:
1. Кузов обладает только инерционными свойствами (не обладает упругими);
2. Элементы подвешивания обладают только упругими свойствами (не обладают инерционными и свойствами трения);
3. Путь абсолютно жесткий (не обладает не инерционными не упругими свойствами);
Уравнение движения:
![]() .
(4.1)
.
(4.1)
Описание неровности 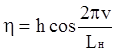 .
.
При движении вагона без отрыва контактных поверхностей колеса рельса колесная пара повторяет рельсовую неровность и процесс её колебаний во времени относительно оси неровности будет иметь вид –
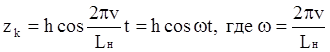 .
.
Заменив в (1) zk представляющим его выражением получим уравнение движения в конкретном виде:
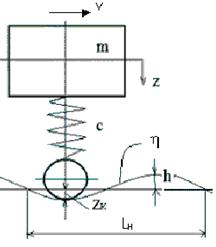
Рис.4.1
Расчетная схема ![]() (4.2)
(4.2)
Разделив
это уравнение на коэффициент при старшей производной и обозначив 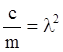 , получим уравнение движения в форме:
, получим уравнение движения в форме:
![]() (4.3)
(4.3)
Общее
решение неоднородного дифференциального уравнения (3)является суммой ![]() , где
, где ![]() –
общее решение соответствущего однородного уравнения, а
–
общее решение соответствущего однородного уравнения, а ![]() –
частное решение неоднородного уравнения (4.3).
–
частное решение неоднородного уравнения (4.3).
Общее решение однородного уравнения имеет вид:
![]() , (4.4)
, (4.4)
где 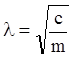 ,
,
![]() -посоянные, подлежащие определению
величины.
-посоянные, подлежащие определению
величины.
Частное решение неоднородного уравнения будем искать в виде:
![]()
Подставим (4) в (3) и
потребуем чтобы левая часть была ровна правой в любой момент времени. Это
требование будет выполнено при условии, что ![]() .
Откуда следует, что
.
Откуда следует, что 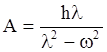 и частное решение
и частное решение
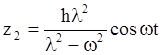 . (4.5)
. (4.5)
Сложив выражения определяющие
![]() , получим общее решение неоднородного
уравнения (3)
, получим общее решение неоднородного
уравнения (3)
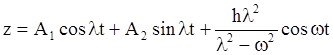 . (4.6)
. (4.6)
Неизвестные амплитуды A1 и A2 найдем задавшись начальными
условиями: t=0, ![]() ,
, ![]() .
.
Использование первого
начального условия дает – 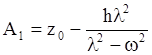 .
.
Использовав второе
начальное условие и первю производную от решения в форме (4.6), получим – 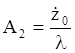 .
.
В результате в окнчательной форме решение примет вид
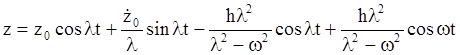 . (4.7)
. (4.7)
Первые
два слагаемых в этом решении – свободные колебания кузова с собственной
частотой ![]() . Они возникают в момент начала движения
только при не нулевых начальных условиях.
. Они возникают в момент начала движения
только при не нулевых начальных условиях.
Третье
слагаемое – колебание кузова с собственной частотой ![]() ,
с амплитудой зависящей только от характеристик возмущающего воздйствия,
возникает всегда в момент начала движения, сопровождая вынужденные колебания, и
называентся сопровждающим колебанием.
,
с амплитудой зависящей только от характеристик возмущающего воздйствия,
возникает всегда в момент начала движения, сопровождая вынужденные колебания, и
называентся сопровждающим колебанием.
Четвертое
слагаемое – колебание кузова с частотой ![]() и
амплитудой зависящей от характеристик возмущающего воздйствия и динамических
характеристик вагона. Это – чисто вынужденные колебания вагона.
и
амплитудой зависящей от характеристик возмущающего воздйствия и динамических
характеристик вагона. Это – чисто вынужденные колебания вагона.
4.2. Процесс биения
Если принять нулевые
начальные условия (t=0, ![]() =0,
=0, ![]() =0.) и достаточную близость
=0.) и достаточную близость ![]() –
–
![]() , где
, где ![]() –
малая величина, то общее решение (4.7) примет вид
–
малая величина, то общее решение (4.7) примет вид
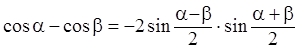
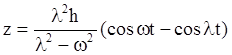 (4.8)
(4.8)
Учитывая тригонометрическое соотношение –
, решение можно представить
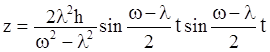 .
.
Принимая, что близость ![]() позволяют записать, что
позволяют записать, что ![]() , тогда решение будет представлять
собой процесс называемый биением, а именно
, тогда решение будет представлять
собой процесс называемый биением, а именно
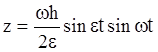 .
.
Решение в данном виде
представляет собой колебательный процесс с частотой ![]() и
переменной амплитудой, изменяющейся по закону синуса с малой частотой
и
переменной амплитудой, изменяющейся по закону синуса с малой частотой ![]() . Графическое этот процесс во времени
представлен на рис.4.2 .
. Графическое этот процесс во времени
представлен на рис.4.2 .
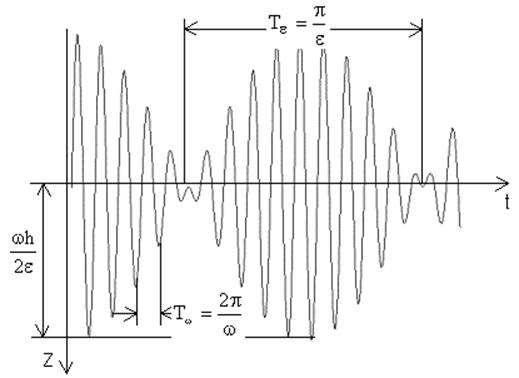 |
Такой колебательный процесс называется биением.
При ![]() , то есть
происходит переход биения в резонанс.
, то есть
происходит переход биения в резонанс.
4.3. Определение темпа роста амплитуды колебаний при резонансе
В
момент весьма близкий к резонансу можно принять – ![]() ,
тогда
,
тогда
процесс вынужденных колебаний будет представлять выражение
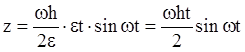 ,
,
Амплидуда этого прцесса прямопропорциональна времени t, то есть растет с течением времени. Графическое этот процесс во времени глядит так:
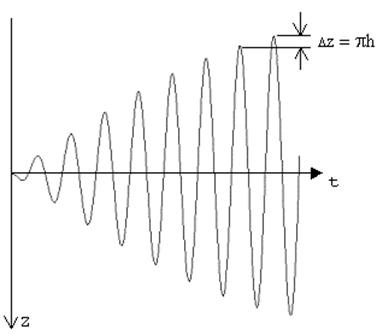
Изменение амплитуды за время равное одному периоду определим как разность
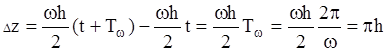
В итоге имеем, что за один период амплитуда кузова возрастет на величину равную амплитуде рельсовой нееровности увеличеной в π раз.
Рис. 4.3. Процесс наростания амплитуды кузова
4.4. Чисто вынужденные колебания вагона
При наличии в подвешивании даже незначительного трения свободные и сопровождающие колебания через несколько периодов затухнут и процесс колебаний кузова будет описываться выражением
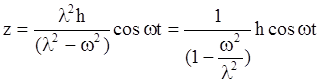 .
.
Обозначив: 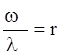 и
и 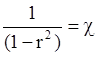 описание
процесса упростится до
описание
процесса упростится до
![]() ,
,
где величина ![]() , зависящая от динвмических
характеристик вагона, характеристик возмущения связанных со скоростью движения,
называется коэффициентом динамичности.
, зависящая от динвмических
характеристик вагона, характеристик возмущения связанных со скоростью движения,
называется коэффициентом динамичности.
 Таким образом, из полученного результата следует, что амплитуда
колебаний кузова равна произведению амплитуды рельсовой неровности на
величину коэффициента динамичности, зависящую от отношения
Таким образом, из полученного результата следует, что амплитуда
колебаний кузова равна произведению амплитуды рельсовой неровности на
величину коэффициента динамичности, зависящую от отношения ![]() , а, следовательно, и от скорости
движения вагона.
, а, следовательно, и от скорости
движения вагона.
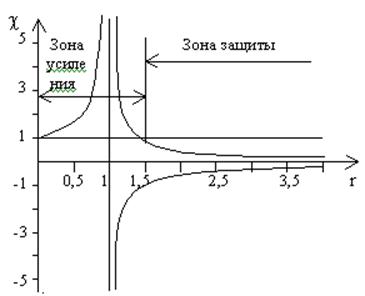
Построим графическое представление этой зависимости.
Кривые на графике построены по следующим значениям:
![]()
![]()
![]()
![]()
![]()
Зона усиления: 0<r<1,41;![]() .
.
Зона
защиты: 1,41<r<![]() ;
; ![]() .
.
В зоне защиты кривая, определяющая величины коэффициента динамичности, перенесена из области отрицательных и в область положительных значений.
В результате можно констатировать, что амплитуда колебаний кузова в зоне усиления превышает величину амплитуды рельсовой неровности, а в зоне защиты может быть значительно меньше её. То есть, желательно эксплуатировать подвижной состав при скоростях движения попадающих в зону защиты. При этом следует иметь в виду, что зону усиления следует проходить как можно быстрее (не давать времени на раскчку кузова в близи резонанса).
При необходимоси эксплуатировать подвижного состава при скоростях движения попадающих в зону усиления необходимо предусмотреть меры по ограничению амплитуда колебаний кузова. К таким мерам в первую очередь относится ведение в рессорное подвешивание вязкого или сухого трения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.