Автоматизированные системы управления технологическими процессами на обогатительных фабриках, страница 5

(М _нач и  t _нач ) в соответствующие уравнения.

Для уравнения (7) решение имеет вид:

а) при

N = N_max -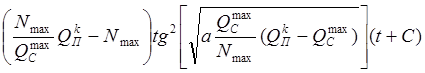

б) при

N = N_max + 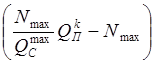th²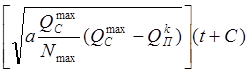

в) при

N = N _max -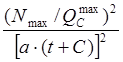

где постоянные интегрирования С определяются подстановкой начальных условий ( М _нач и t _нач ) в соответствующие уравнения.

В решениях (9) и (12) используется функция th , когда:

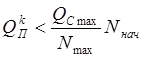 и функция cth когда: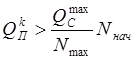

б) - увеличение нагрузки агрегата в устойчивой области

  = 98  т  / ч;   M _Н  = 40 т ; N_П  = 775 кВт;

в) - переход из неустойчивой области в устойчивую при уменьшении нагрузки

  = 80  т  / ч;   M _Н  = 75 т ; N_П  = 1300 кВт;

г) - уменьшение нагрузки в устойчивой области

  = 80  т  / ч;   M _Н  = 60 т ; N_П  = 1375 кВт;

д) - увеличение нагрузки агрегата в неустойчивой области

  = 98  т  / ч;   M _Н  = 75 т ; N_П  = 1300 кВт;

е) - движение в вершину статической характеристики из устойчивой области

  = 100  т  / ч;   M _Н  = 55 т ; N_П  = 1300 кВт;

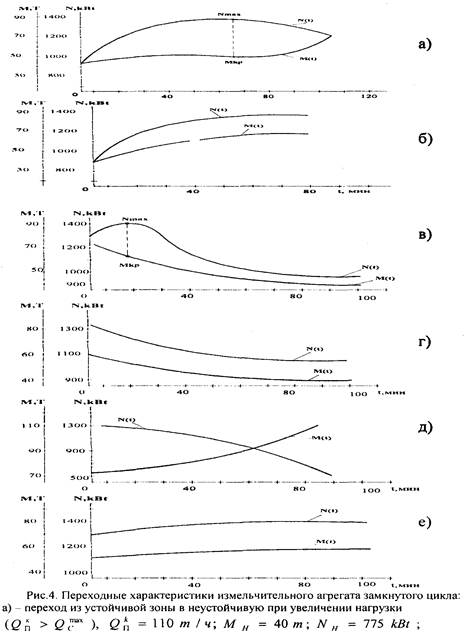
На рис.4 показаны некоторые переходные процессы, найденные с помощью решений (8) - (9). В этих графиках задана условно - численная функция вычисленная экспериментально:

         N  = f(М) = 1400 + 1,00(М - 65)²,

где N _max = 1400 кВт,  М_Кр = 65 т/ч,  а = 1,00 кВт / т².

На рис.4, а показано движение агрегата из состояния с координатами

          М _н = 40 т; N _н = 775 кВт; и Q_Cн = 37,5 т  / ч                               при возмущении исходным питанием до  = 110 т / ч. Величина М начинает быстро увеличиваться, но при подходе к М_Кр  её рост замедляется, а при прохождении состояния с величиной запаса М_Кр снова начинает расти и через некоторое время агрегат попадает в аварийное состояние. Величина N в начала растёт, достигает точки максимума 1400  кВт при запасе М_Кр  и дальше начинает быстро уменьшаться. Агрегат перегружается.

На рис. 4, б показано движение агрегата из того же состояния, что и в предыдущем примере

(М_Н = 40 т, Q_Сн, = 37,5 т / ч, N_H = 775 кВт), но при Q^k_П=98 т/ч Величины М_Н и N_Hвозрастают, стремясь к равновесному состоянию с величиной запаса  М = 59,72 т.  и  N=1372  kBm.

На рис.4 в движения начинается из состояния с координатами М_Н = 75 т, Q_Сн = 90 т / ч,  и  N_Н = 1300 кВт при  = 80 т/ч Поскольку (Q_П < Q_С), величина М непрерывно уменьшается, причём до момента достижения критической величины М_Кр  величина N растёт, достигая своего максимального значения 1400 кВт, а затем начинает уменьшаться. В окрестностях точки с запасом 

М_Кр  скорость изменения величины запаса максимальная, а в начале и в конце движения она значительно меньше. Заканчивается движение в точке с координатами М = 48,3 т,

 N = 1120  kBm.

На рис.4, г-д, е  представлены движения величин N(t) и M(t) соответственно при уменьшении нагрузки агрегата в устойчивой области, при увеличении - в неустойчивой и движение в вершину статической характеристики из устойчивой области.

Рассмотренные примеры дают представление о характере переходных процессов в агрегате самоизмельчения. Они иллюстрируют решение уравнений (6), (7) при скачкообразном изменений величины Q_П.

Функции N = f(M) и Q_С  = f(N) аппроксимированы соответственно параболой (4) и прямой линией (5). Это допустимо при рассмотрении движений, которые «не удаляют» агрегат на большое расстояние от экстремумов характеристик N_max , М_кр, Например, при рассмотрений случаев рис.4, а, д  решения уравнений имеют разрыв на конечном интервале времени. Здесь введённая аппроксимация уже недостаточна и требуется вводить более точное отражение функций N = f(M) и Q_C = f(N). Тем не менее, полученные решения достаточно хорошо отражают физические процессы, происходящие в агрегате и согласуются с экспериментальными данными.

Постоянная интегрирования  С  во всех уравнениях измеряются в единицах времени, и означает степень удалённости начала движения от особых точек функций, описывающих это движение (полюсов или нулей). Для решений, показанных на рис.4, постоянные времени  С  одинаковы.