![]() = (QП – QС)
= (QП – QС)![]() t , где
t , где ![]() М
- изменение запаса материала в мельнице за время
М
- изменение запаса материала в мельнице за время ![]() t , т; QП - скорость подачи исходного питания, т/ч;
t , т; QП - скорость подачи исходного питания, т/ч;
QС-производительность по готовому продукту, т/ч.
Производя перегруппировку членов и переходя к пределу, получаем:
dM / dt = QП – QС.(1)
Из уравнения (1) видно, что приращение массы материала в мельницу равно разности между расходом руды в питании QПи расходом на выходе агрегата QС .
Для условий равновесия приращение массы материала
dM / dt = 0 ; в этом случай запас материала в мельнице не изменяется и равен заданному M = Mgag.
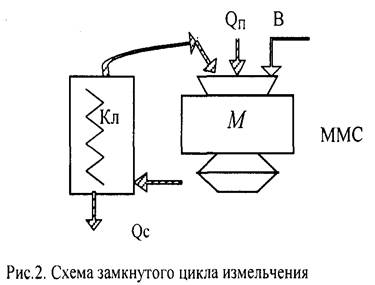
MМС - мельница мокрого самоизмельчения; Кл - классификатор; Qп - скорость подачи исходного питания, т/ч; qс - производительность по сливу (готовому продукту), т/ч; М - запас материа-ла в агрегате; В - вода.
В переходном режиме изменение скорости питания мельницы Qп уравновешивается изменением производительности мельницы Qс , а также увеличением или уменьшением запаса материала в мельнице dM / dt. Перепишем уравнение (1) в виде: dM / dt + QС = QП.Необходимо определить, как изменяются во времени величины М и QСпод влиянием QП , т.е. получить дифференциальные уравнение объекта по этим каналам уравнения. Для этого надо найти зависимость вида:
QС = f (М).
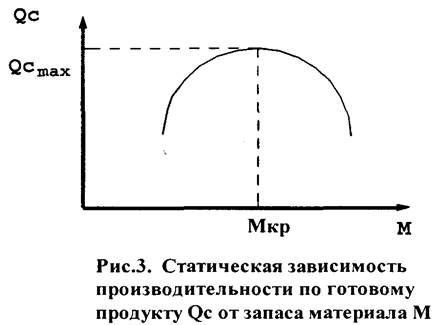
Эта зависимость для мельниц самоизмельчения имеет вид параболы с координатами максимума статической характеристики в точке QСmax , MКр (рис. 3).
Работа
левее точки экстремума соответствует устойчивому режиму агрегата, прав![]() ее - неустойчивому.
ее - неустойчивому.
При условии нормальной работы измельчительного агрегата в установившемся режиме на устойчивой ветви статической характеристики QС= f (М) величины QП , М и QС
получают малые приращения, поэтому, применив принцип линеаризации, можно записать:
QС = K1 * ![]() M(2)
M(2)
Откуда после подстановки в (1) и переходя к пределу получим:
T ![]() + M = kQП(3)
+ M = kQП(3)
где Т - постоянная времени, ч;
K=1 / K1 - коэффициент передачи, ч.
Постоянная времени Т = ![]() M / AQC показывает способность мельницы
накапливать и расходовать запас материала М. Поскольку величины QCи
М практически трудно измерить, то для управления
процессом самоизмельчения обычно используют косвенный параметр - мощность,
потребляемую двигателем мельницы N. Тогда QCможно выразить
как функцию
M / AQC показывает способность мельницы
накапливать и расходовать запас материала М. Поскольку величины QCи
М практически трудно измерить, то для управления
процессом самоизмельчения обычно используют косвенный параметр - мощность,
потребляемую двигателем мельницы N. Тогда QCможно выразить
как функцию
QC= f (N).
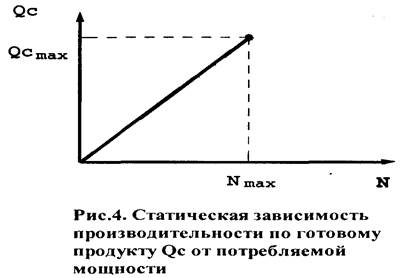
График функции Qc = f(N) (рис.4) представляет из себя прямую линию, проходящую через начало координат, уравнение которой для удобства будем представлять так:
QC = ![]() N . (4)
N . (4)
Аппроксимируем зависимость N = f (M) параболой вида:
N = Nmax - a(M – M Кр)2 (5)
где [а] - коэффициент формы параболы, кВт/т2 . Тогда с учётом (4) уравнение (1) запишется как:
![]() = QП – QC = QП -
= QП – QC = QП - ![]() N =
N =
= QП - ![]()
![]() .
(6)
.
(6)
Уравнение (6) может быть выражено через управляемый выходной параметр N; для этого необходимо продифференцировать выражение (5) по времени t, что даёт:
![]()
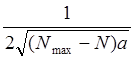
![]() = QП -
= QП - ![]() N (7)
N (7)
Величина
QПв этих уравнениях может быть любой
функцией времени; рассмотрим решение их для случая скачкообразного изменения QП . В этом случае решения уравнений (6) и (7)
могут быть найдены методом разделения переменных. Обозначим ![]() величину QПпосле её скачкообразного изменения в
начальный момент времени, Nначи М нач - величины
N и М в начальный момент времени (начальное условия). Знание
начальной величины QП при этом необязательно.
величину QПпосле её скачкообразного изменения в
начальный момент времени, Nначи М нач - величины
N и М в начальный момент времени (начальное условия). Знание
начальной величины QП при этом необязательно.
Основные расчётные уравнения
Решения уравнения (6) имеют следующий вид:
a) для ![]() >
> ![]()
M = MКр + 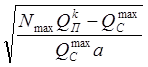 tg
tg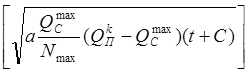 (8) б) для
(8) б) для ![]() <
< ![]()
M = Mкр - 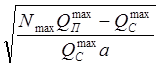 th
th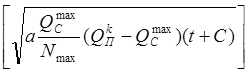 (9)
(9)
в) для ![]()
M
= M Kp - 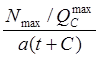 (10)
(10)
где С в уравнениях (8)![]() (10) - постоянные
интегрирования, которые определяются подстановкой начальных условий
(10) - постоянные
интегрирования, которые определяются подстановкой начальных условий
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.