Автоматизированные системы управления технологическими процессами на обогатительных фабриках

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт имени Г.В.Плеханова                                                                                                            

(технический университет)

                                  Кафедра обогащения полезных ископаемых

                  АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

                                 ТЕХНОЛОГИЧЕСКИМИ      

    ПРОЦЕССАМИ  НА  ОБОГАТИТЕЛЬНЫХ ФАБРИКАХ

                                Методические указания к лабораторным работам

                                     для студентов дневной и заочной форм

                                           обучения специальности 090300

САНКТ-ПЕТЕРБУРГ

2003

УДК 622.7 (075.83)                                                                        

            АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ НА ОБОГАТИТЕЛЬНЫХ

ФАБРИКАХ: Лабораторные работы / Санкт-Петербургский горный ин-т. Сост.:

, СПб, 2003 27с.

Цель лабораторных работ - ознакомление со свойствами различных технологических объектов (как линейных, так и нелинейных), их статикой и динамикой, изучение способов составления и решения уравнений динамики.

Лабораторные работы предназначены для студентов специальности

090300 "Обогащение полезных ископаемых"

Ил. 11  Табл.5.

Научный редактор проф.

© Санкт-Петербургский горный институт им. Г.В. Плеханова, 2003

Работа 1. ИССЛЕДОВАНИЕ ОБЪЕКТОВ С ПОТОКОМ И

ЗАПАСОМ НА ПРИМЕРЕ ГИДРАВЛИЧЕСКОГО ОБЪЕКТА

Цель работы:

Получение статистических и динамических характери

стик расчетным методом.

Необходимое оборудование:

Персональный компьютер

Общие сведения:

Уравнение материального баланса для гидравлического

Объект (аккумулятора)

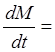                                    Q_П- Q_Р

или                                                                          (1)

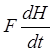                                   = Q_П – Q_Р

где F - площадь поперечного сечения бака, м ; - запас жидкости в баке, м³; Q_n-вход объекта; Н-выход объекта. По

скольку 

откуда 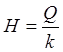 ,уравнение (1) приводится к виду:

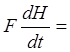Q_П– kHили  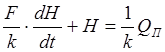                         (2)

где 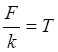 - постоянная времени объекта, с;

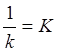- коэффициент передачи обьекта, с / м²;

Произведём разделение переменных

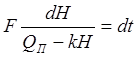
и проинтегрируем выпажение

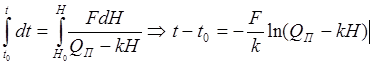
После преобразований получим:

;

;

;

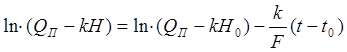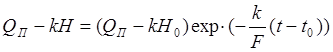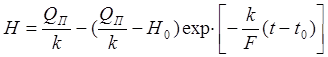Окончательно имеем:

                 (3)

Уравнение (3) показывает закон изменения во времени

(динамику) уровня жидкости в баке Н (выходной величины) при скачкообразном изменении притока жидкости Q_n(входной величины), когда выходная величина в момент подачи возмущения не равна нулю (Н = Н₀ ).

Легко видеть, что при t=t₀, т.е. в начальный момент времени Н = Н₀, так как exp[-(k / F)*(t - t₀)]. При t получим ехр [- ( k / F) * (t - t₀ )]   0, а Н  H_П , т.е. уровень в баке стремится к установившемуся значению, Н_П  когда приход равен расходу  Q_П = Q_Р .

Из уравнения (3) следует, что если Н₀  > Н_П (это значит, что Q_Р  > Q_П), то из бака будет вытекать жидкости больше, чем туда поступает, и уровень в баке будет понижаться; если

H₀ < Н_П (т.е. Q_P < Q_П), то уровень в баке будет повышаться.

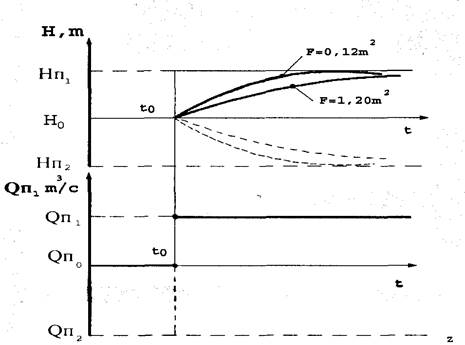
  Рис.1. Разгонные кривые гидравлического объекта

Эти два случая соответствуют двум графикам переходного процесса в гидравлическом объекта (рис.1).

Таким образом, кривая изменения переходного процесса в гидравлическом объекте начинается с Н=Н₀ и асимптотически

(при t) приближается кН _П = kQ_П.Такая кривая носит название экспоненты. При Н₀ = 0 уравнение (3) переходит к виду:

                  (4)

а при t₀ = 0 ещё более упрощается:

                     (5)

Итак, мы установили, что каждому притоку Q_П(вход)

соответствует свой уровень Н (выход), такой объект называется объектом с самовыравниванием. Зависимость Н = f(Q_П) называется статической характеристикой объекта, а вида

Н = f(t) - динамической характеристикой (рис.1).

Для нахождения динамической характеристики достаточно определить постоянную времени Т и коэффициент передачи К.

Это можно сделать путем снятия кривой разгона. Тогда

К = Н_П / Q_П , а Т  определяется как подкасательная к экспоненте

(рис.1). Если значения коэффициента передачи и постоянной времени известны заранее, то можно, пользуясь уравнением (3), построить кривую переходного процесса Н = f(t) по точкам.

Статическая характеристика Н = f(Q_П) получается как огибающая функции для найденных экспериментально нескольких пар установившихся значений Q_П , Н_П .

Пример расчета переходных характеристик объекта:

Рассчитать разгонные кривые гидравлического объекта при следующих исходных данных:

            К = 0.12 м²/с; F₁ = 0.12 м²; Н₀ = 1.2 м; Н_П1 = 1.5 м;