Selection and Sizing of Autogenous and Semi-Autogenous Mills. Pilot Plant Testwork Basis, страница 8

Power Equations

The question of which comes first in the sequence of mill design, applied power or mill size, can best be approached by referring to some basic (but similar) power equations. Traditionally, net mill power is expressed as

kW = 2π·N·τ                                                                               (1)

Where:        N   = mill speed, rpm

τ  = torque developed by the mill charge as its centre of gravity changes position from rest

= 

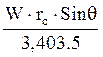
W  = mill charge weight, kg

Where:        r_c   = radius to the mill charge centre of gravity, m

  = angle of r_с to the vertical

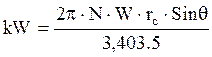                                                                (2)

But this only expresses power as a function of the mill charge weight in a mill of a given size. It does not, as Morrell points out (Morrell 1992, 1996), take into account the contributions to power draw made by:

·  The imprecise position of the centre of gravity of the mill charge; i.e., it is never known, physically

·  Attrition

·  Abrasion

·  Friction and rotation within the mill charge

·  Heat and sound emanating from the mill charge and within the mill itself

·  Wind loss

·   Bearing friction

·  Size analysis of the mill charge (and new feed)

·  Shape of the mill charge.

In Morrell's methodology, and as output from JK SimMet simulations:

kW (gross)   =                                (3)

Where:        D                  =  Effective mill diameter (inside shell liners), m

L_e                = Effective grinding length expressed as the length of an equivalent mill cylinder to include the volume of the conical ends, m

ρ_c                 = density of the total mill charge, t/m3

a, δ              = Non-linear functions of total mill filling and mill speed,

respectively

K                 = constant selected from a database to reflect losses associated with movement of the mill charge

kW (no-load) =                                             (4)

Where:        Nc               = fraction of critical speed

So far, from these equations, mill power is derived from a mill size and its contents. Such mill power is very dependent upon the value of "K", which is selected from Ж Tech's database of operating mills. It is conceivable that the mill size could be predicted with confidence from a calculated power value (based on grinding testwork) if a reliable value of "K" was available to the user.

Mill Sizing

Mill suppliers use similar but proprietary equations that estimate net power draw, or in reverse estimate mill size. Much depends upon the exponent which is applied to the "Diameter, D" and also which "Diameter" is used: diameter at the mill shell plate or, more usually, an effective mill diameter which takes into account the thickness of the shell liner plates plus the thickness of the shell lifters averaged (or "smoothed") over the mill circumference, and for which the exponent 2.5 is developed from applied mathematics and is unalterable in modem technology. Also important in this context are the equations that are used to calculate the mill charge density and whether changes in mill speed are considered to be directly proportional and independent of total mill charge volume.

For dry grinding, the following formula has been proposed (Turner 1982):

kW (Net)       =     2.208 · p · D^2.5 · L · N_c                                                                                                (5)

Note that Turner specified dry mills to run at 84.5% C.S., and also that N_c is an independent factor. The value 2.208 looks like a power number.

Note that the combination of К, а, and 5 in equation 3 looks like a power number.

Another approach and, in the authors' opinion, a more accurate and although an empirical one is based on Loveday's definition of power number (Loveday 1978). Power number is derived from the following equation:

kW(Net) =                                                                 (6)

Where        ρ_c                 = mill charge density, t/m3