







Очевидно, что
матрица (12.40 является симметричной, так как ![]() Коэффициенты
корреляции, составляющие эту матрицу, характеризуют тесноту линейной связи
между двумя величинами, входящими в систему, без учета возможного влияния на
эту связь остальных n-2 величин, их влияние просто игнорируется.
Поэтому коэффициенты корреляции
Коэффициенты
корреляции, составляющие эту матрицу, характеризуют тесноту линейной связи
между двумя величинами, входящими в систему, без учета возможного влияния на
эту связь остальных n-2 величин, их влияние просто игнорируется.
Поэтому коэффициенты корреляции ![]() называются
парными, а матрица (1.4) – матрицей парных коэффициентов корреляции.
Естественно, что все свойства коэффициентов корреляции, перечисленные выше,
остаются в силе, но подчеркнем еще раз, парные коэффициенты корреляции
учитывают не чистую линейную связь между двумя величинами, а как бы смешанную с
влиянием на эту пару других величин системы (13.1). Встает задача»очистить»
коэффициенты корреляции от этого влияния. Для этого рассмотрим систему n-1
случайных величин
называются
парными, а матрица (1.4) – матрицей парных коэффициентов корреляции.
Естественно, что все свойства коэффициентов корреляции, перечисленные выше,
остаются в силе, но подчеркнем еще раз, парные коэффициенты корреляции
учитывают не чистую линейную связь между двумя величинами, а как бы смешанную с
влиянием на эту пару других величин системы (13.1). Встает задача»очистить»
коэффициенты корреляции от этого влияния. Для этого рассмотрим систему n-1
случайных величин
![]()
которая получается из системы (12.1) исключением Xi.
Найдем по методу наименьших квадратов приближение Xj как линейной функции остальных n-2 случайных величин системы (13.5) т.е.
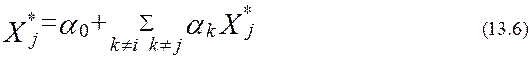
Здесь знак суммирования означает, что сумма находится для всех Xk, кроме Xj и Xj, т. е. если, например,i<j, то
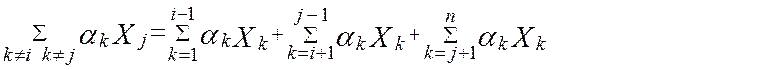
Коэффициенты регрессии αk находятся в соответствии с (9.2) как координаты точки минимума функции
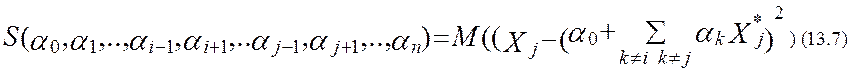
Аналогично, исключив из системы (13.1) Xj , найдем приближение Xj как линейной функции остальных n-2 величин
X*1=β0+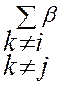 kXk
(13.8)
kXk
(13.8)
Теперь найдем остатки величин Xi и Xj
Zi(j)=Xi-X*I, (13.9
Zj(i)=Xj-X*j. (13.10)
Это остатки после исключения линейного влияния n-2 величин.
Определение 1. Коэффициент корреляции между остатками называется частным коэффициентом корреляции между самими величинами. Он обозначается pij,
pij=p(Xi,Xj)=r(Zi(j),Zj(i)). (13.11)
Частные коэффициенты корреляции характеризуют тесноту линей связи между двумя случайными величинами системы после исключения линейного влияния остальных величин, входящих в эту систему. Частные коэффициенты корреляции обладают всеми 10-ю свойствами коэффициентов корреляции. Можно доказать, что частные коэффициенты корреляции выражаются через парные формулой
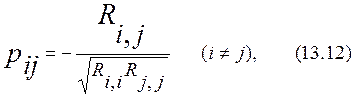
где Ri,j , Ri,i , Rj,j – алгебраические дополнения соответствующих элементов матрицы R (13.14). Естественно положить при I=jpi,j=1. Тогда частные коэффициенты тоже образуют симметричную матрицу
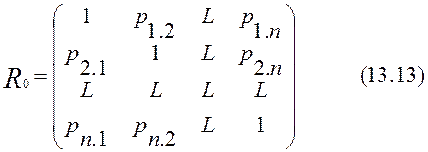 .
.
Рассмотрим для примера систему трех случайных величин, имеющих матрицу парных коэффициентов корреляции R, причем сразу учтем ее симметричность
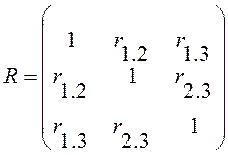
Найдем алгебраические дополнения элементов r1.2 , r1.1 и r2.2 этой матрицы
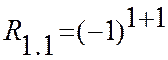
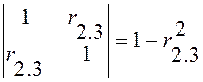
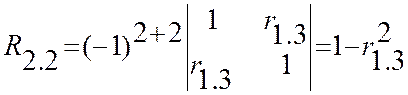
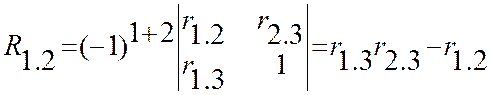
тогда на основании (13,12) получим
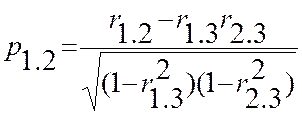 ,
,
и, аналогично в силу симметричности можно написать
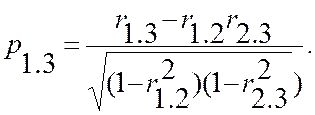
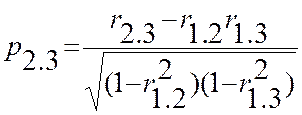
Вернемся к рассмотрению системы (13,1) и найдем методом наименьших квадратов приближение Xi в виде линейной функции остальных случайных величин этой системы. Для этого минимизируем выражение
![]()
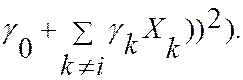
Найдя значения ![]() , обеспечивающие минимум этого выражения, мы
получим приближение Xi в виде линейной функции остальных случайных величин системы (13,1)
, обеспечивающие минимум этого выражения, мы
получим приближение Xi в виде линейной функции остальных случайных величин системы (13,1)
X$i 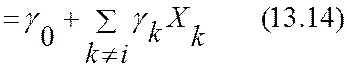
Коэффициент
корреляции между ![]() и величиной (13,14)
называется множественным ил суммарным коэффициентом корреляции.
Он обозначается ri ,
и величиной (13,14)
называется множественным ил суммарным коэффициентом корреляции.
Он обозначается ri , 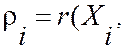 X$i), (i=IKn). (13.15)
X$i), (i=IKn). (13.15)
Аналогично частным коэффициентам корреляции множественные коэффициенты корреляции тоже могут быть выражены через парные
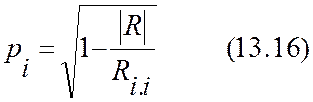 ,
,
где ![]() - определитель матрицы R
(12.4);
- определитель матрицы R
(12.4);
![]() – алгебраическое дополнение
элемента ri,i этой матрицы.
– алгебраическое дополнение
элемента ri,i этой матрицы.
Множественные коэффициенты составляют неслучайный вектор.
(![]() (13.17)
(13.17)
Множественный коэффициент корреляции
характеризует тесноту линейной связи между одной из случайных величин и всеми
остальными в совокупности. Его значение не меньше нуля, т.е. p1![]() 0, поэтому не все свойства коэффициентов корреляции
справедливы для него. Так, если pi =0, то Xi некоррелирована с остальными случайными
величинами системы. Если же pi=1, то Xi
является линейной функцией остальных случайных величин системы. В случае же,
если 0<
0, поэтому не все свойства коэффициентов корреляции
справедливы для него. Так, если pi =0, то Xi некоррелирована с остальными случайными
величинами системы. Если же pi=1, то Xi
является линейной функцией остальных случайных величин системы. В случае же,
если 0<![]() <1, то между
<1, то между ![]()
![]() и остальными случайными величинами
системы существует корреляционная связь, причем di= 100p2 показывает какой процент вариации Xi вызван линейным влиянием остальных случайных величин
в совокупности.
и остальными случайными величинами
системы существует корреляционная связь, причем di= 100p2 показывает какой процент вариации Xi вызван линейным влиянием остальных случайных величин
в совокупности.
Найдем формулы для вычисления множественных коэффициентов корреляции для системы трех случайных величин.
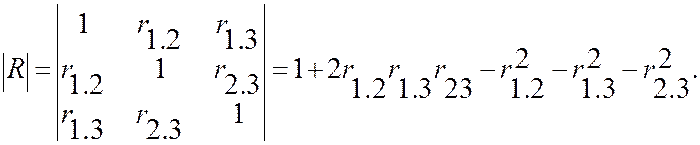
Учитывая, что R1.1=1-r22.3, по формуле (13.16) получим
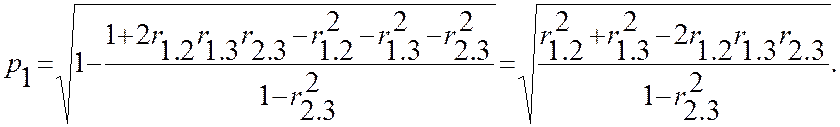
Аналогично
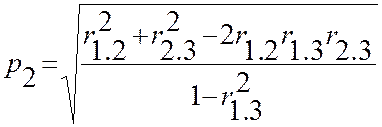
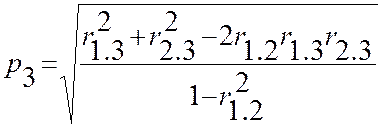
Пример 5. Рассмотрим систему трех случайных величин, которая характеризуется матрицей парных коэффициентов корреляции
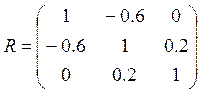
которая по парным коэффициентам корреляции имеет некоррелированные величины X1 и X3. Найдем частные коэффициенты корреляции
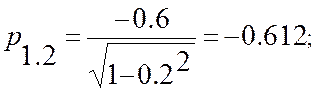
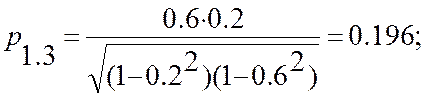
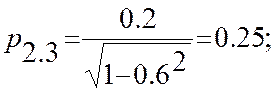
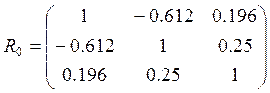
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.