Таким образом, частные коэффициенты корреляции показывают, что, после исключения линейного влияния X2, фактически некоррелированность между X1 и X3 отсутствует. Найдем множественные коэффициенты корреляции
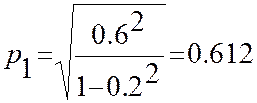
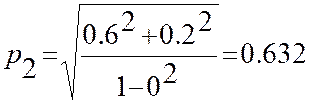
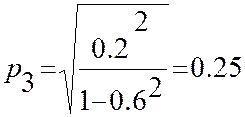
14. Оценки параметров системы двух случайных величин
Перейдем к решению некоторых задач математической статистики, а именно к оценке параметров. Как Вы должны помнить, в основе математической статистики лежит выборочный метод. Выборку можно рассматривать как дискретное приближение исследуемой величины. Оценкой параметра случайной величины является аналогичный параметр выборки. Например, оценкой математического ожидания, т.е. среднего значения случайной величины, является среднее арифметическое выборки. Как Вы, конечно, помните, оценка считается «хорошей», если она является несмещенной, эффективной и состоятельной. Все эти соображения сохраняются и в случае, если речь идет о системах случайных величин. Что же представляет собой выборка, если объект исследования – система случайных величин? Вспомним, что каждое значение системы – это точка n-мерного пространства. Поэтому каждый элемент выборки при анализе системы двух случайных величин (X,Y) представляет собой пару чисел. Выборка объема n реализуется в виде последовательности пар чисел
![]() (14.1)
(14.1)
Очевидно, что оценки математических ожиданий и дисперсий каждой из величин по результатам этой выборки можно вычислить по формулам, которые были выведены при статистическом анализе одной случайной величины
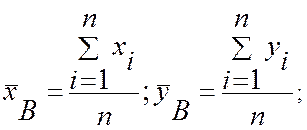
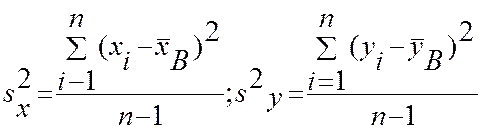
Аналогично тому, как была получена формула несмещенной оценки дисперсии, можно показать, что несмещенная оценка корреляционного момента находится по формуле
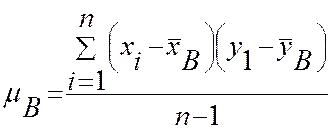 ,
,
и тогда оценка коэффициента корреляции, выборочный коэффициент корреляции, можно найти по формуле
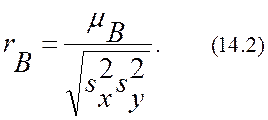
Умножив в (14.2) числитель и знаменатель на n-1 и сделав несложные преобразования, аналогичные тем, что были произведены при доказательстве первого свойства дисперсии и свойства корреляционного момента, можно получить формулу
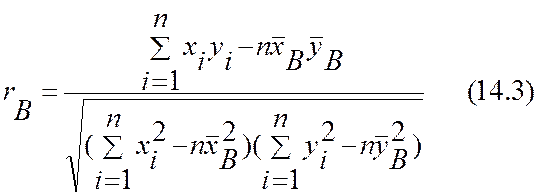 .
.
Упражнение 2.Самостоятельно
получить формулу (14.3) из (14.2) при этом учесть, что 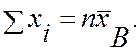
Среди пар чисел, составляющих выборку (14.1) могут быть и повторяющиеся, поэтому выборку можно задать в виде табл.7.
Таблица 7
|
X |
Y |
n |
|
|
|
|
|
L |
L |
L |
|
|
|
|
|
L |
L |
L |
|
|
|
|
Имеется в виду, что в выборке (14.1) k
различных пар, ni – частота пары (![]() ),
причем
),
причем 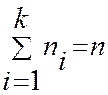 - объему выборки. В этом случае
формула оценки коэффициента корреляции имеет
- объему выборки. В этом случае
формула оценки коэффициента корреляции имеет
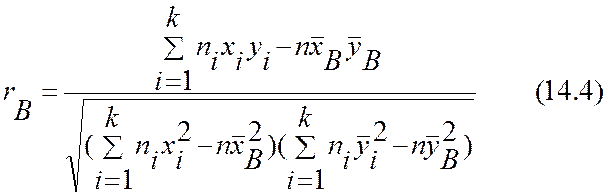 .
.
Среди пар (![]() )
в табл.7 нет одинаковых, но среди значений
)
в табл.7 нет одинаковых, но среди значений ![]() и
и
![]() могут быть одинаковые, поэтому
выборку можно оформить в виде табл.8, аналогичной табл.1.
могут быть одинаковые, поэтому
выборку можно оформить в виде табл.8, аналогичной табл.1.
Таблица 8
|
X Y |
|
L |
|
L |
|
|
|
|
L |
|
L |
|
|
L |
L |
L |
L |
L |
L |
|
|
|
L |
|
L |
|
|
L |
L |
L |
L |
L |
L |
|
|
|
L |
|
L |
|
В табл. 8 указано v
различных значений величины X и w различных значений величины Y,
![]() - частота пары (
- частота пары (![]() ). В этом случае оценка коэффициента
корреляции может быть найдена по формуле
). В этом случае оценка коэффициента
корреляции может быть найдена по формуле 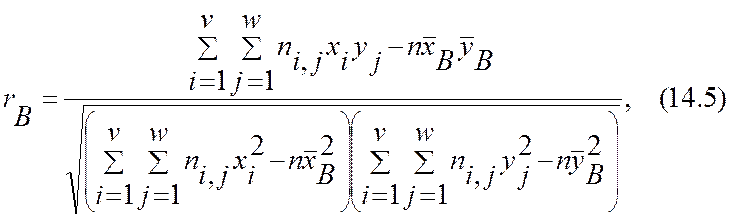 ,
,
Упражнение 3. Написать формулы нахождения средних выборочных и исправленных выборочных дисперсий для выборок, заданных табл.7 и табл.8.
Пример 6. Дана выборка объема n=10
(1,1),(1,2),(1,1)(1,2).(2,1),(2,2),(2,3),(1,2),(2,2),(2,2)
Составим таблицу типа табл.7.
Таблица П5
|
X |
Y |
N |
|
1 |
1 |
2 |
|
1 |
2 |
3 |
|
2 |
1 |
1 |
|
2 |
2 |
3 |
|
2 |
3 |
1 |
Из этой таблицы составим таблицу типа табл.8
Таблица П6
|
X Y |
1 |
2 |
3 |
|
1 |
2 |
3 |
0 |
|
2 |
1 |
3 |
1 |
Упражнение 4. Найти оценку
коэффициента корреляции по выборке, приведенной в примере 6. (Ответ ![]() =0,33).
=0,33).
15. Оценки параметров системы k случайных величин.
Пусть выборка объема n
производится для исследования системы k случайных
величин (![]() ). Каждый элемент выборки
представляет собой k чисел
). Каждый элемент выборки
представляет собой k чисел
![]() (i=1,…,n),
(15.1)
(i=1,…,n),
(15.1)
где ![]() - значение
случайной величины Xj в i-м элементе выборки. Очевидно. Средние
выборочные. Исправленные выборочные дисперсии и оценки парных коэффициентов
корреляции находятся по формулам
- значение
случайной величины Xj в i-м элементе выборки. Очевидно. Средние
выборочные. Исправленные выборочные дисперсии и оценки парных коэффициентов
корреляции находятся по формулам
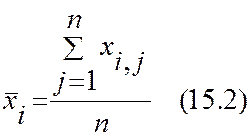 ,
,
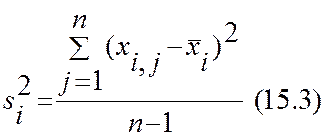
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.