Экзамен. Система уравнений Максвелла.
(один из основных вопросов курса)
Уравнения Максвелла справедливы для переменных электромагнитных полей.
R|div Dc h = 4πρ
|||Srot
Ec
h = −![]() 1⋅ ∂B
1⋅ ∂B
c ∂t
— система уравнений Максвелла в
|div Bc h = 0
|
T||rot Hc h = 4πj
+ ![]() 1⋅ ∂D c c ∂t
1⋅ ∂D c c ∂t
дифференциальной форме.
R|div Dc h = ρ |||Srot Ec h = − ∂B
∂t
В системе СИ: . |div Bc h = 0
|
T||rot Hc h = j + ∂D
∂t
Чтобы уравнения имело смысл решать относительно электрического и магнитного полей, нужно дополнить их так называемыми материальными связями:
D =εE
,
B =µH которые нужно дополнить законом Ома j =λE , если токи не заданы явным образом.
R|SD =εε00 E
В системе СИ: B = µµH .
T|j =λE Кроме того, заряды и токи связаны уравнением непрерывности: c h ∂ρ
div j + = 0
∂t
Для решения задач обычно удобнее использовать уравнения Максвелла в интегральной форме:
R||zcD
dS, h =
4πQ
S
![]()
![]()
z E
dll 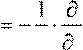 zcB
dS, h
|S
zcB
dS, h
|Szl c h c t
S
![]() | B dS, = 0
| B dS, = 0
|
| |
S
T||z H
dll 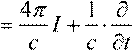 zcD
dS, h
zcD
dS, h
lS
Прокомментируем каждое из 4-х уравнений.
Первое из уравнений Максвелла можно записать в виде ΦD = 4πQ. Для полей независящих от времени — это электростатическая теорема Гаусса. Для переменных полей теорема доказана быть не может, но Максвелл предположил, что равенство остается верным и для переменных полей. Все следствия из этого предположения согласуются с опытом.
Второе уравнение rot Ec h = −![]() 1⋅ ∂B — обобщение Максвелла закона c ∂t
1⋅ ∂B — обобщение Максвелла закона c ∂t
![]() электромагнитной
индукции Фарадея Eинд = −1 ⋅ dΦB . Заметим, что
закон c dt
электромагнитной
индукции Фарадея Eинд = −1 ⋅ dΦB . Заметим, что
закон c dt
Фарадея содержит полную производную, а уравнение
Максвелла в интегральной форме 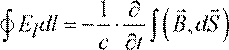 содержит
частную производную
содержит
частную производную
l S
от потока ΦB = ∫(B dS, ) по времени. Дело в том, что изменение потока при S
движущемся контуре дает вклад в э. д. с. индукции Eинд = E ≡ ∫(Eстор,dl )
l
через силы Лоренца FЛ , которые рассматриваются, как сторонние силы с
![]() напряженностью Eстор =
FЛ =
напряженностью Eстор =
FЛ =
![]() 1c V B, , но не дает вклад в
циркуляцию q
1c V B, , но не дает вклад в
циркуляцию q
|
d |
E dl, i поля E , поэтому в циркуляцию дает вклад только частная производная
l по времени.
Третье уравнение ΦB = 0 означает отсутствие магнитных зарядов.
Четвертое уравнение rot Hc h = 4πj
+ ![]() 1⋅ ∂D представляет собой теорему о
1⋅ ∂D представляет собой теорему о
c c ∂t
циркуляции поля в магнитостатике дополненное токами смещения Максвелла.
Факультативная вставка.
R|div Dc h = 4πρ
c ∂t
Система уравнений Максвелла — это 8 |div Bc h = 0
|
T||rot Hc h = 4πj
+ ![]() 1⋅ ∂D c c ∂t
1⋅ ∂D c c ∂t
одномерных уравнений для 6-и одномерных неизвестных E и B.
Система уравнений избыточна. В системе дифференциальных уравнений для нескольких функций одной переменной, как и для системы обычных алгебраических уравнений, нужно чтобы число уравнений совпадало с числом неизвестных. Произвол, который содержится в решении дифференциальных уравнений с одной переменной, — это несколько произвольных констант интегрирования, их число равно сумме порядков старших производных в уравнениях.
Если же решаются дифференциальные уравнения в частных производных, то произвол решений гораздо больше. Для устранения произвола могут потребоваться дополнительные дифференциальные уравнения. Тем не менее, в случае электромагнитных полей система действительно избыточна.
Дело в том, что уравнения не нужны, так как являются div B = 0
![]() R||Srot
Ec
h = −1⋅ ∂B
R||Srot
Ec
h = −1⋅ ∂B
c ∂t
следствием другой пары уравнений .
![]() T||rot
Hc
h = 4πj
+ 1⋅ ∂D c c ∂t
T||rot
Hc
h = 4πj
+ 1⋅ ∂D c c ∂t
И действительно. Рассмотрим
дивергенцию от уравнения rot Ec h = −![]() 1⋅ ∂B .
1⋅ ∂B .
c ∂t
Дивергенция ротора любого поля равна нулю:
![]() div
rot Ed
c hi = e∇ ∇, ,E j = eE,
∇ ∇, j = cE,0h = 0, где использовано
то, что циклическая перестановка векторов в смешанном скалярно-векторном
произведении e∇ ∇, ,E j
не изменяет его величину. Тогда 0 =
div rot Ed c hi =
divFGH−
div
rot Ed
c hi = e∇ ∇, ,E j = eE,
∇ ∇, j = cE,0h = 0, где использовано
то, что циклическая перестановка векторов в смешанном скалярно-векторном
произведении e∇ ∇, ,E j
не изменяет его величину. Тогда 0 =
div rot Ed c hi =
divFGH−![]() 1⋅ ∂BIJK = −
1⋅ ∂BIJK = −![]() 1⋅ ∂ div Bc h
=>
1⋅ ∂ div Bc h
=>
c ∂t c ∂t
−![]() 1⋅ ∂ div
Bc
h = 0
=> div Bc h =
const — дивергенция поля B c ∂t не изменяется
со временем.
1⋅ ∂ div
Bc
h = 0
=> div Bc h =
const — дивергенция поля B c ∂t не изменяется
со временем.
Если когда-то в рассматриваемой области не было магнитного поля B, то и его дивергенция была равна нулю div Bc h = 0, а затем дивергенция не могла измениться. Следовательно, div Bc h = 0.
Аналогично из уравнения rot Hc h = 4πj
+ ![]() 1⋅ ∂D можно получить
1⋅ ∂D можно получить
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.