Теорема о циркуляции электростатического поля Е. Ротор. Теорема Стокса (математическая теорема, без доказательства)

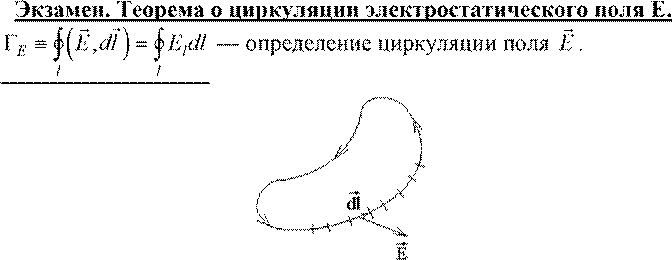
Для вычисления циркуляции по контуру или замкнутой линии эту замкнутую линию нужно разбить на большое число малых отрезков. Каждому отрезку соответствует вектор dl . В области отрезка электрическое поле E почти постоянно. Для каждого отрезка нужно вычислить dE dl, i и просуммировать соответствующие величины по замкнутому контуру.  Рассмотрим циркуляцию поля E по замкнутому контуру:

                                                            F'            1                   1            1

        Γ_E ≡ zdE dl, i = ^zF^GH ,dl I^JK = ^zl dF dl', i = ^zl dA =               A_I→I

                             _l                        l      q'            q'                   q'            q'

Работу по перемещению заряда по замкнутому контуру A_I→I можно найти из выражения для работы по перемещению из точки I в точку II:

                                                                                   1      1

       AI→I = AI→II  II→I = q'∑qiFHG iI − IKJ = 0        =>

                                                                      i           r      riII      II→I

            Γ_E = 0 или, что то же самое, zdE dl,           i = 0 — теорема о циркуляции

l

электростатического поля.

Факультатив. Ротор.

                                                                                       ∂A     ∂A             ∂A     ∂A             ∂A                                                          ∂A

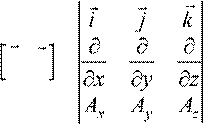rot Ac h ≡ ∇_{, A} =          = _i ⋅HF^{G z} − ^y KJI + _j ⋅FH     ^x −  ^z KI + _k ⋅HF^{G                 y} −    ^x I^JK

                                                                                        ∂y      ∂z              ∂z      ∂x             ∂x                                                           ∂y

Факультатив. Теорема Стокса. (математическая теорема, без доказательства)

    zd_{rot A dS}c h, i = zdA dl, i,

                S                                   l

 

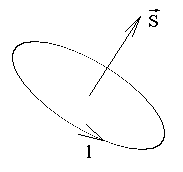
Направление нормали к поверхности и направление обхода контура образуют правый винт.

          Вместо доказательства сравним два равенства:  z f dx'       = _{f b}a f− _{f a}a f b

a

        ze ∇, A dS, j = zdA dl,      i

                S                                  l

В обеих формулах интеграл от производной равен сумме значений функции по границе области интегрирования.

Факультатив. Физический смысл ротора.            Рассмотрим маленькую площадку S :

 zdrot A dSc h, i = zdrot Ac hⁱndS ≈ drot Ac hⁱn ⋅zdS ≈ S ⋅drot Ac hⁱn  => rot A dSc h, i zdA dl, i

                                 SS                                                                             S

Γ

                drot Ac hⁱn ≈^S= ^l                           =    ^A

                                                         S                   S           S

          Ротор — поверхностная плотность циркуляции.

Циркуляция — мера закрученности поля.           Ротор производная вида:

 

Экзамен. Теорема о циркуляции электростатического поля E в дифференциальной форме.

По теореме о циркуляции электростатического поля для любого контура l :

1 _l             S

        zdE dl, i = 0       ⋅                  S → 0         =>

       drot Ec hⁱn = 0 — для любого направления вектора нормали n . Тогда

      rot Ec h = 0

Экзамен. Скачок электростатического поля E при переходе через заряженную поверхность.

Этот же вопрос можно было бы назвать "граничные условия для поля E в вакууме", так как заряженную поверхность можно рассматривать, как границу двух объемов.

          Вблизи любая поверхность выглядит плоской.

Рассмотрим скачок поля E на плоской поверхности с поверхностной плотностью заряда σ.

Рассмотрим цилиндр малой высоты с основаниями параллельными заряженной плоскости. Пусть основания цилиндра расположены с двух сторон от заряженной плоскости.

 

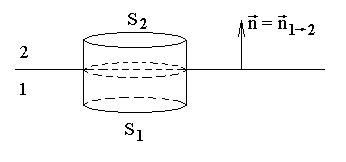
Если высота цилиндра мала, то потоком через боковую поверхность можно пренебречь. Тогда

          4πσ⋅S = 4πQ = Φ ≈ Φ_S2 + Φ_S1 = E S_2n − E S_1n ,

где минус в последнем выражении вызван тем, что внешняя нормаль к цилиндру на площадке S₁ противоположна выбранному направлению нормали к заряженной плоскости n = n_{1 2→} .

          Сравнивая конец и начало цепочки равенств, получим

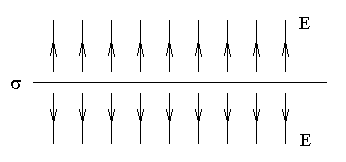
 E S_2n − E S_1n = 4πσ⋅S  =>  E_2n − E_1n = 4πσ,

где нормаль к границе n смотрит из объема 1 в объем 2.      В частности бесконечная заряженная плоскость

 

--------

Рассмотрим теперь тангенциальную (по касательной к поверхности) составляющую поля E при переходе через заряженную границу.

Рассмотрим прямоугольный контур в плоскости перпендикулярной заряженной поверхности.

 

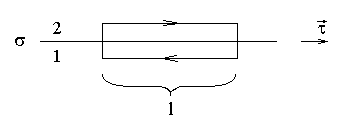
Если высота прямоугольника мала, то вклад в циркуляцию вертикальных отрезков пренебрежимо мал. Тогда

        ΓE ≈ Γ2 + Γ1 = E2l ⋅l + E1l ⋅l = E l2τ − E l1τ , где минус вызван тем, что на нижнем отрезке направление dl противоположно выбранному направлению единичного тангенциального вектора τ.

    По теореме о циркуляции электростатического поля E имеем Γ_E = 0.

Тогда с учетом Γ_E = E l_2τ − E l_1τ получим:

          E2τ − E1τ = 0.

                    Здесь τ — единичный вектор по касательной к заряженной поверхности.

Экзамен. Три формы электростатической теоремы Гаусса и теоремы о циркуляции.

            zcE dS^, h = 4πQ

|SS c h

div E = 4πρ — электростатическая теорема Гаусса в интегральной, |

T|E_2n − E_1n = 4πσ дифференциальной формах и для границы раздела.

^R||SzE dlc h_l       = 0

l

rot E = 0     — теорема о циркуляции электростатического поля