Обобщение Максвелла закона электромагнитной индукции Фарадея. Коэффициент взаимной индукции

Экзамен. Обобщение Максвелла закона электромагнитной индукции Фарадея.

(для второй половины закона Фарадея)

Максвелл предположил, что изменение магнитного поля вызывает появление вихревого электрического поля, и это поле приводит к появлению

Eинд.

Рассмотрим два выражения для э. д. с. индукции.  С одной стороны:

         E_инд ^≡ _∫(E_стор,dl ) ⁼ _∫(E dl, ),    где    по     предположению                           Максвелла

                                  l                             l

E E⁼ _стор. По теореме Стокса zdE dl, i ⁼ zdrot E dSc h,     i, тогда

                                                                               l                        S

         ^E_инд ⁼ _∫(rot E( ),dS).

S

          С другой стороны по закону Фарадея:

           E_инд ^{= −1}c ^{⋅ d}Φdt^{B = −1}c ^⋅ ∂Φ∂_t^B , здесь полная производная по времени

заменена частной, чтобы подчеркнуть неподвижность контура, неизменность его пространственных координат. Тогда  Eинд = −1 ⋅ ∂∂t ∫dΦB = −1c ⋅ ∂∂t ∫(B dS, ) = S∫−1c ⋅ ∂∂Bt ,dS . c

                                                 S                            S

          Приравниваем два выражения для э. д. с. индукции и получаем:

    zdrot E dSc h, i = ^zF_HG−¹⋅ ^∂B _,dSI^JK             _=>    ^zS drot Ec hindS = ^zS F^GH−¹⋅ ^∂BI^JK dS _,

_S             S             c ∂t    c ∂t n            где S — любая поверхность.

          Пусть S — маленькая площадка, тогда интеграл можно заменить одним слагаемым:          drot Ec hin ⋅_S = −FGH ¹⋅ ^∂BIK^Jn ⋅_{S           =>}      drot Ec hin = −FH^{G 1}⋅ ^∂BI^JK c ∂t      c ∂t n

          для проекции на любое направление n . Следовательно,

                           rot Ec h = −¹⋅ ∂^B — математическая формулировка обобщения Максвелла c ∂t

закона электромагнитной индукции Фарадея.

∂B

                    ≠ 0 — это только первый шаг к рассмотрению переменных

∂t электромагнитных полей. Второй шаг (токи смещения) будет сделан позднее.  В электростатике rot Ec h = 0. Для переменных полей rot Ec h ≠ 0 и поле E

— вихревое, не потенциальное поле.

Экзамен. Коэффициент взаимной индукции.

(в присутствии линейных магнетиков)

Линейность магнетика означает, что связь между векторами B и H линейна: B H= µ .

     Рассмотрим систему контуров и два контура из этой системы l_i и l_k .

 

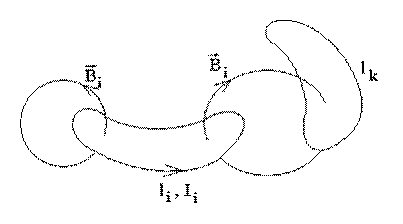
    Пусть ток I_i протекает в контуре l_i . Ток I_i создает магнитное поле B_i .

Это поле пронизывает контур l_k .

            Пусть Φ_ki — поток магнитного поля B_i через контур l_k .

            Φ_ki ~ B_i ~ I_i                     =>

                         Φ_ki = L_ki ^Ii — определение коэффициента взаимной индукции L_ki . c

          В системе СИ:      Φ_ki = L I_{ki i} .

Факультатив. Коэффициент взаимной индукции двух катушек на общем сердечнике при µ>>1.

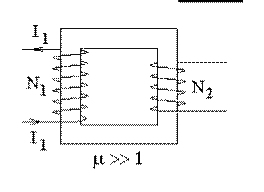
          Найдем коэффициент взаимной индукции L₂₁ .

            Схема решения задачи: I₁ → H₁ → B₁ →Φ₂₁ → L₂₁ .

Коэффициент взаимной индукции L₂₁ не зависит от величин токов в обеих обмотках.

Пусть в первичной обмотке протекает ток I₁ . Будем считать, что во вторичной обмотке тока нет, например, потому что эта обмотка замкнута через очень большое сопротивление.

     Рассмотрим теорему о циркуляции напряженности магнитного поля

           H dll      = 4πI lc

для контура интегрирования вдоль оси сердечника. Поле H во всех сечениях сердечника примерно одинаково и направлено по оси сердечника, поэтому для сердечника длиной l получим:

 Hl = 4πN I1 1 => H = 4πN I1 1 => B = µH = 4πµN I1 1 => c cl cl

           Φ21 = BS N⋅ 2 = 4πµN N S1    2      ⋅ I1

                                                                 l           c

          Тогда    с    учетом    определения    коэффициента    взаимной        индукции

Φ₂₁ = L₂₁ ^I1 получим c

          L21 = 4πµN N S1 2   

l

          Заметим, что L₂₁ = L₁₂ .

           В системе СИ: zH dl_l   = I               B = µ₀µ⋅ H           Φ₂₁ = L I_{21 1}

l

                                                                         µ0µN N S1       2

                                         L21 =                   .

l

Экзамен. Теорема о равенстве коэффициентов взаимной индукции.

(теорема о взаимности)

           Lki = Lik

Докажем это равенство только для токов в вакууме без магнетиков, хотя это равенство справедливо и в присутствии магнитных сред.

                   Заметим, что равенство C_ki = C_ik тоже называют теоремой о взаимности.

Получим некоторое равенство для потока магнитного поля через площадку S , равенство, которое нам понадобится и в других вопросах.

         Φ_B = zcB dS,       h

S

Подставим сюда B = rot Ac h и получим  Φ_B = zdrot A dSc h, i.

S

    По теореме Стокса zdrot A dSc h, i =zdA dl, i, тогда

                                                                 S                                   l

           Φ_B ⁼dA dl,       i, где l — контур, ограничивающий площадку S , через

l

которую проходит поток Φ_B . Это равенство нам понадобится сейчас и далее.

Рассмотрим теперь поток Φ_ki магнитного поля тока в i -ом контуре через k -ый контур:

         Φ_ki =zdA dl_i ,       _k i

lk

          Подставим сюда определение векторного потенциала dA = ^Idl и получим