Механическая работа магнитных сил взаимодействия системы токов без учета взаимодействия каждого контура с самим собой

Экзамен. Механическая работа магнитных сил взаимодействия системы токов без учета взаимодействия каждого контура с самим собой.       Как и в предыдущем вопросе, работа э. д. с. индукции в каждом контуре с током не учитывается.

Пусть dA_ki — работа, совершаемая магнитными силами над k -ым контуром со стороны магнитного поля  тока i -го контура.

                   Будем считать, что k ≠ i. Работу dA_ii рассмотрим отдельно в следующем

вопросе. Итак k ≠ i. Используя формулу dA = ^I ⋅ Φd _B , получим

c

                      dA_ki = ^Ik ⋅dΦ_ki = ^Ik ⋅d LFH ki ⋅ ^Ii IK . c  c         c

                                              Формально     d LFH ki ⋅ ^Ii IK = ^Ii ⋅dL_ki + L_ki ⋅d ^Ii ,        как     дифференциал      от c    c        c

произведения. Однако, слагаемое L_ki ⋅d ^Ii означает изменение тока I_i и вместе c

с ним магнитного поля без перемещения k -го контура. Как было замечено в предыдущем вопросе, работа при этом не совершается, поэтому нужно

отбросить слагаемое L_ki ⋅d ^Ii и оставить только ^Ii ⋅dL_ki . Следовательно c       c

Ik ⋅ Ii ⋅dLki

  dAki = c c

Казалось бы, работа взаимодействия системы токов будет равна dA ⁼ ∑ ∑dA_ki = ^{I Ik i}₂ ⋅dL_ki , однако на самом деле работа вдвое меньше.

              i k,                 i k,    c

          Рассмотрим подробнее.

L_ki может изменяться и за счет перемещения k -ого контура (обозначим  такое изменение, как d L_{k ki} ) и за счет перемещения i -ого контура (обозначим такое изменение, как d L_{i ki} ). Тогда

dL_ki = d L_{k ki} + d L_{i ki} — изменение коэффициента взаимной индукции при перемещении обоих контуров.

Работа при перемещении k-го контура в поле i-го контура dA_ki связана с изменением коэффициента взаимной индукции L_ki только за счет перемещения k-го контура, тогда

          dAki = Ik ⋅ Ii ⋅d Lk      ki вместо прежнего выражения dAki = Ik ⋅ Ii ⋅dLki . c    c        c        c

          Рассмотрим сумму двух слагаемых

                                dAki + dAik = I Ik i2 d Lk            ki + I Ii k2 d Li            ik . c        c

           С учетом L_ik = L_ki получим

                                dAki + dAik = I Ik i2 d Lk     ki + I Ik i2 d Li ki = I Ik i2 ⋅bd Lk            ki + d Li            ki g = I Ik i2 ⋅dLki  => c   c        c        c

dAki + dAik = I Ik i2 ⋅dLki

c

Просуммируем это равенство по всем значениям индексов i и k , таких что i ≠ k , и получим

∑ ∑ ∑ I Ik i ⋅dLki .            dAki + dAik = 2 i k,        i k,               i k,          c i k≠     i k≠         i k≠

      Здесь в левой части равенства каждая из двух сумм равна dA. Тогда

  dA = ¹∑ ^{I Ik i}₂ ⋅dL_ki — механическая работа взаимодействия системы

2 i k, c

i k≠

токов без учета работы каждого контура над самим собой.

Факультатив. Механическая работа магнитных сил контура с током над самим собой при деформации контура.

          Антипараллельные токи отталкиваются, поэтому контур с током стремится растянуться в окружность. Если ему позволить, то он совершит положительную работу.

            Мысленно разобьем контур с током I на сумму N токов I_i = ^I . Пусть

N

эти токи полностью тождественны и занимают один и тот же объем.

N

         Покажем, что ∑ A_ii ^→_N→∞ 0.

i=1

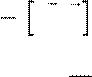           dF = ^I ⋅ dl B,      =>      dF_i ~ B I_{i i}

c

1

           Но B_i ~ I_i ~      , тогда

N

1           dFi ~ B Ii i ~ 2              => N N ∑ Aii = NAii ~ 1 →N→∞ 0 i=1              N

1 Aii ~ dFi ~  2 N

=>

          Тогда для системы тождественных токов при N → ∞ можно пренебречь работой самовоздействия каждого тока и найти работу по формуле из предыдущего вопроса:

        dA ≈ 1∑ I Ik i2 dLki

 c

      Здесь все слагаемые одинаковые, так как токи тождественны, тогда

                                                                                                            I     I

                                                                                                                 ⋅                    2

            dA = 1 N Na −1f I Ik i2 dLki = 1 N Na −1f N 2N dL ≈ 1 ⋅ I2 ⋅dL                    =>

                            2                 c              2                   c               2 c

1  I ²

               dA =    ^⋅ ₂ ⋅dL — работа контура с током I над самим собой, dL —

2  c

изменение индуктивности контура при его деформации.

         dA = 1∑ I Ik i dL + 1∑ Ii2² dLii

                                            2          ki

                            2 i k,     c                2 i c

i k≠

Здесь первое слагаемое — работа взаимодействия системы токов без учета работы каждого контура над самим собой, второе слагаемое — работа каждого контура над самим собой.

          Объединяя оба слагаемых в одну сумму, получим

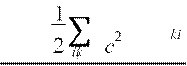          dA =         ^{I Ik i} ⋅dL — эту формулу для работы нужно запомнить к экзамену без ее вывода.

Факультатив. Магнитная энергия взаимодействия системы токов.

(с учетом работы э. д. с. индукции)  Пусть W — магнитная энергия системы токов.

При уменьшении энергии магнитного поля энергия расходуется на механическую работу магнитных сил и на работу ^E_k I dt_k э. д. с. индукции в каждом контуре. Э. д. с. индукции черпают энергию из магнитного поля. Работа э. д. с. индукции расходуется на Ленц-Джоулево тепло в соответствии с законом Джоуля-Ленца N = EI +UI = EI .

          −dW = dA ⁺ ∑E_k I dt_k

k

Тогда подставим выражение для работы dA из предыдущего вопроса и получим  dW = − ^{1 I I} dL − E_k I dt_k .

                                  2 i k,    c               k

Подставим сюда выражение для э. д. с. индукции E ^{= −1⋅ d}Φ и получим c      dt

  dW = − 1∑ I Ik i2 dLki − ∑FH−1⋅ dΦk IKI dtk     .

                                  2 i k,    c               k          c     dt

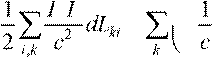                                                   Сократим dt в числителе и знаменателе, тогда F   I

          dW = −          ^{k i}             −       −  ⋅dΦ_k KI_k .

   Подставим сюда выражение для потока через коэффициент взаимной

индукции Φ_k ⁼ ∑ L_ki ^Ii и получим

                                          i            c

  dW = − 1∑ I Ik i2 dLki + ∑ ∑Ik ⋅dFHG   Lki Ii IJK .

                                  2 i k,    c                k c          i            c

                                           F  Iⁱ I

Разложим d LH ki K , как дифференциал от произведения и получим