Линии поле E не рвутся. Теорема Ирншоу. Потенциальность кулоновских сил. Потенциальная энергия заряда в электростатическом поля

Факультатив. Линии поле E не рвутся.

Если в объеме нет зарядов Q = 0, то Φ_E = 4πQ = 0. Поток равен нулю – это значит, сколько линий поля втекает в объем, столько и вытекает.

Следовательно, линии поля E не начинаются и не заканчиваются в пустом объеме без зарядов. В этом смысле линии поля E не рвутся. Как выяснится позднее, это справедливо и для переменных электрических полей.

 

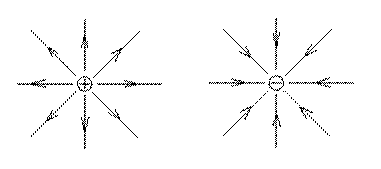
Линии поля E вытекают из положительных зарядов и втекают в отрицательные заряды. В этом смысле заряды буквально являются источниками поля.

Экзамен. Теорема Ирншоу.

Невозможно статическое распределение зарядов, в котором хотя бы один заряд находится в устойчивом равновесии.

          Отметим, что неустойчивое равновесие возможно, например:

 

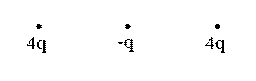
          Доказательство.

          Проведем доказательство методом "от противного".

Предположим, что для одного из зарядов есть устойчивое равновесие и получим противоречие.

          Будем считать, что все заряды дискретные - точечные.

Пусть в устойчивом равновесии находится заряд q , например положительный.

Для устойчивого равновесия поле сил при смещении в любую сторону пытается вернуть заряд в точку равновесия. Тогда поле сил F остальных зарядов в окрестности заряда q имеет следующий вид:

 

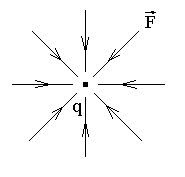
          Аналогично     выглядит     и     поле      E      остальных    зарядов,                кроме

F

рассматриваемого заряда q , так как E =  .

q

          Рассмотрим маленькую сферу вокруг заряда q :

 

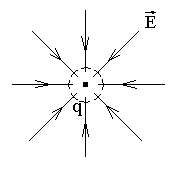
      Из рисунка видно, что поток поля E через эту сферу отрицательный

Φ_E < 0. Это с одной стороны, а с другой стороны поток равен нулю Φ_E = 0. И действительно, внутри малой сферы вокруг заряда q нет других зарядов, и для них Q = 0. Следовательно, для поля E остальных зарядов, кроме q , получим Φ_E = 4πQ = 0.

^RSΦ_E < 0 TΦ_E = 0

          Итак               . Полученное противоречие доказывает теорему.

Экзамен. Потенциальность кулоновских сил.

Поле сил потенциально (силы консервативны), если работа по перемещению пробного заряда не зависит от траектории, а зависит только от начальной и конечной точек.

Докажем сначала потенциальность сил со стороны поля точечного заряда q . Найдем работу электростатических сил при перемещении пробного заряда q' из точки I в точку II:

 

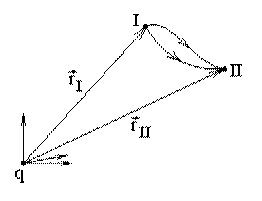
Пусть начало координат совпадает с зарядом q . Найдем работу dA на малом участке пути dl :

                             dA = F dl',    i d= q E dl'        ,         i = q E dl'        ⋅         _E = q E dl'    ⋅         _r ≈ q E dr' ⋅         = q' ₂ dr . q r

 

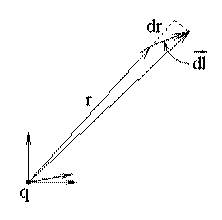
          Из рисунка видно, что dl_r ≈ dr .

          Работа на конечном участке

II                       rzII              rzII        FH     IK rII               FGH     IJK q     dr       1        1          1

             A_I→II =dA =      q' ₂ dr = q q'     2 = q q'      −= q q'         −              =>

                                          Ir_I                  r                r_I r                 r rI                           rI       rII

                                              1     1

            A_I→II = q q' F^GH  − I_KJ — работа по перемещению пробного заряда q' в поле

                                             rI       rII

заряда q из точки r_I в точку r_II , если начало координат совпадает с зарядом q.

Это выражение не зависит от формы траектории, следовательно, поле E точечного заряда потенциально.

Докажем теперь потенциальность сил произвольного распределения точечных зарядов.

          Из принципа суперпозиции

rII

         E = ∑E_i zq' ,d⋅ dl i   =>

ir_I

          zII q E dl'd ,      i = ^∑zq E dl'd _i ,   i             => r       ^rII

                rI                                        i    rI

                                                                                  1      1

    AI→II = ∑ Ai I, →II = ∑q q' iFHG  −  IJK

r     r ii        iI             iII

                                        A_I→II = q'∑q_i ^GH⁻  I_KJ — работа по перемещению пробного заряда q' из  1 1

                                          i           riI       riII

точки I в точку II. Здесь r_iI = r_I − r_i — вектор из i-го заряда в точку I, r_iII = r_II − r_i

— вектор из i-го заряда в точку II.

Экзамен. Потенциальная энергия заряда в электростатическом поля.    Энергия — это способность совершить работу, поэтому:

           WI ≡ AI→∞.

Электростатическая энергия заряда в точке I по определению равна работе электростатических сил по перемещению заряда из точки I на бесконечность.

                                                                                 FGH 1 1 IJK       1             1

            WI ≡ AI→∞ = AI→IIII→∞ = q'∑i qi riI − riII  riII →∞ = q'∑i qi riI = q'∑i qi rI − ri

=>                                W rf = q^'∑i q_i r _{− r}i - энергия заряда q' в точке с радиус-вектором r в 1

поле остальных зарядов q_i .

Экзамен. Потенциал электростатического поля.

          Потенциал — потенциальная энергия единичного заряда.

 ϕ≡              

Экзамен. Потенциал произвольного распределения зарядов.

Для системы точечных зарядов q_i получим следующее выражение для потенциала ϕ в точке с радиус-вектором r :

W ra f  q  ϕ_r ≡ = ∑ ⁱ q'       _i r − r_i

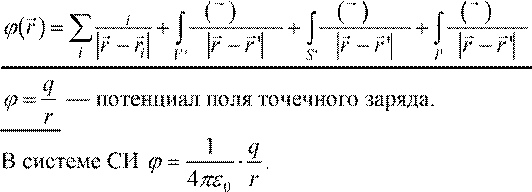 Тогда для произвольного распределения зарядов получим: q ρr' ⋅dV' σ r' ⋅dS' τ r' ⋅dl'

                                                                                           S '                             l'

Экзамен. Связь потенциала и напряженности электростатического поля. b gI            b gI              I              zI dF dl',     i _∞z_I ^FGH K^IJ ∞zd   i

∞

                ϕr    ≡ W r    ≡ A →∞ =                =      F',dl    =    E dl,           =>

                                      q'          q'             q'               q'            _I

∞ ∞ r   r

 ϕa fr = zdE dl, i = z E dl_l                                    — связь потенциала и напряженности в одну

сторону.

Получим теперь связь между E и ϕ в другую сторону.  Рассмотрим  _{ϕ ϕ}b gr_II − b gr_I = z E dl_l − z E dl_l = −z E dl_l .

                                                   ∞                ∞                    r_II

                                                   rII                     rI                            rI

           Устремим r_II → r_I и получим:

ϕ ϕ ϕbrII g − brI g ≈ d U|V       l

          ^rz^II l                  l      W|     =>      dϕ= −E dl            =>

− E dl ≈ −E dl

r_I

           — для любого направления l .

           Рассмотрим направления вдоль осей x,y,z:

                           ∂ϕ

E_x = −

∂x

|S _y ∂ϕ | _∂ T|Ez         

             E = −                 =>

                |      ∂y

                                                                                                   ∂ϕ ϕ ϕ∂  ∂

             E = E_x ⋅i + E_y ⋅ j + E_z ⋅k = −F⋅i +        ⋅ j +    ⋅kIK^J = −∇ϕ, где

                                                                                        ∂x        ∂y         ∂z

∂       ∂       ∂ ∂x  ∂y      ∂z

          ∇ ≡ i      + j      + k     — оператор набла.

        grada^{ϕ ϕ}f ≡ ∇ — определения градиента.

^R|S|Ea f= −∇z^ϕ l

∞         — связь напряженности и потенциала в обе стороны. ϕr = E dl

r

                         W             F'

 ϕ≡           и E ≡ и из ϕa fr = z E dl_l мы получили E = −∇ϕ.

                          q'             q'                      _r

∞

          Тогда, повторив выкладки, мы из равенства _{W r}a f = zdF dl,                                                  i получим