Вектор Пойнтинга. Примеры движения энергии электромагнитного поля. Разряд конденсатора через сопротивление

Факультатив. Вектор Пойнтинга.

(вектор Умова-Пойнтинга)

Хотя вопрос и факультативный, но окончательное выражение для вектора Пойнтинга и его физический смысл нужно знать к экзамену.

Вектор Пойнтинга — это плотность потока энергии электромагнитного поля или энергия, которая в единицу времени протекает через единичную площадку, перпендикулярную направлению движения энергии.

Энергия в некотором объеме уменьшается, если она вытекает через границу объема.

          Для количественного рассмотрения вопроса рассмотрим объемную плотность энергии электромагнитного поля, которая равна сумме энергий электрического и магнитного полей:

cD E, h   cB H, h   w =    +       .

8π 8π

          Рассмотрим изменение энергии, например, электрического поля:

              F^G_HcD E, h^IJK    ₁ oc  h c ht

                          dw d⁼    =       D dE, + E dD,     . 8π 8π

Два слагаемых в этой сумме одинаковы по величине. И действительно, для линейного, возможно, анизотропного диэлектрика

          D =ε^ɵ E         => D_k ⁼ ∑ε_kiE_i           =>

Fi

         cD dE, h = ∑D dE_{k k} = ^{∑ ∑}_HG i ε_kiE dE_iIK^J    k = ^∑k i ε_kiEdE_{i    k}

                                         k                          k                                             ,

         cE dD, h = ∑EdD_{i i} = ∑i Ed_i F^GH∑k ε_ik E_k I^JK = ^∑k i ε_ik EdE_{i            k}

                                         i                                                                        ,

         С учетом ε_ki =ε_ik получаем cD dE, h⁼cE dD, h. Тогда

         dw = cE dD,    h.

         Аналогично для энергии магнитного поля dw = cH dB, h.

           dw 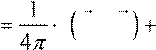o E dD, cH dB, ht — изменение объемной плотности энергии электромагнитного поля. Эта формула справедлива в более общем случае, чем

                                                           cD E, h cB H, h               ¹ oc    h c                      ht

исходная формула w =               +             . Формула dw =        ^⋅       E dD,                                          ⁺ H dB,                    

                                                                          8π 8π                                4π

справедлива и в случае нелинейной зависимости индукции поля от напряженности и в случае гистерезисной зависимости.

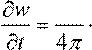                                      Тогда   1 R^SF^GHE_,^∂_∂^D_t I^JK ⁺ FGHH_,^∂_∂^B_t I^JKUWV, куда в правую часть производные T

по времени можно подставить из уравнений Максвелла

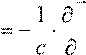
             R||rot Ec hB                          R|∂

                      St                                 => |S ∂Dt = c rot H⋅                 c h− 4πj        =>

    T||rot Hc h 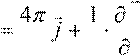c     c         Dt    T||∂∂Bt = −c rot E⋅   c h

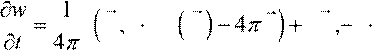
  { E c rot H     j         dH               c rot Ec hi}               =>

            = cE j, h−  {dE rot H, c hi −dH rot E, c hi}       =>

_t

                 ∂∂^w cE j, h− ^c_π{eE, ∇,H j e− H, ∇,E j}

          −      =

                        _{t                  4}

Здесь           подчеркнуты        величины,   на      которые действует    оператор дифференцирования ∇ .

          В        обоих          смешанных           скалярно-векторных произведениях     сделаем циклические перестановки векторов так, чтобы вектор ∇ оказался на первом месте, а затем в первом векторном произведении поменяем местами векторы с изменением знака произведения. Тогда

                 ∂∂^w c j E, h+ ^c_π{d∇, E,H i d+ ∇, E,H i}.

          −      =

                        _{t                  4}

Два слагаемых в фигурных скобках можно объединить, как производную от произведения:

          −      =

                 ∂∂^wt c j E, h+ 4^c_πd∇, E H,        i,

где убраны подчеркивания, так как производные берутся от всех величин, которые стоят за знаком производной ∇ .

 Скалярное произведение вектора ∇ на какой-либо другой вектор — это дивергенция другого вектора, тогда  − ∂∂^w = c j E, h+ divFH ₄^c_π E H, IK .

_t

          Тогда

          −      =

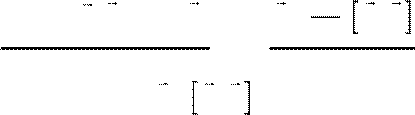                 ∂∂^wt c j E, h+ div Sc h, где S ≡ 4^cπ⋅ E H,               — вектор Пойнтинга. Эти два равенства нужно помнить к экзамену без доказательства.

           В системе СИ: S ≡ E H,  .

                                             ∂∂^wt            c j E, h+ div Sc h можно уточнить с учетом возможных

           Равенство −       ⁼

сторонних сил с напряженностью E_стор .

Рассмотрим закон Джоуля-Ленца в дифференциальной форме с учетом сторонних сил:

 ν⁼ ( j E,        + E_стор)                    =>    ( j E, ) =ν⁻( j E, _стор) =>

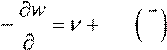         ( j E, _стор)           div S

t

         Это же уравнение в интегральной форме примет следующий вид:

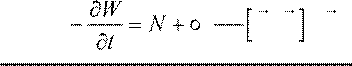 ∑i Ei iI                        zS FH 4cπ E H dS,         ,         IK , где в единицу времени энергия э. д. с. и энергия поля расходуются на нагрев (Ленц-Джоулево тепло) и вытекает через границу объема. Эту формулу тоже нужно знать к экзамену без доказательства. Здесь E_i — любые э. д. с., кроме э. д. с. индукции, работа которых учитывается изменением энергии электромагнитного поля.

Из последней формулы следует физический смысл вектора Пойнтинга. Вектор Пойнтинга — это плотность потока энергии или энергия, которая в единицу времени протекает через единичную площадку перпендикулярную направлению движения энергии.  Заметим, что для одного фотона

         W = mc^{2 U}V              W     hν

                     =>      p =    =   . p = mc W  c        c

R|^|SS = ^c E H, 4π

                      Из равенств  следует, что

T||p = W c

           S = ¹ ⋅ E H, — плотность потока импульса. c 4π

Факультатив. Примеры движения энергии электромагнитного поля.

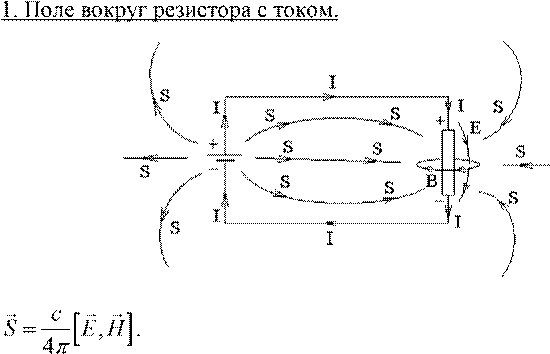
Линии поля S втекают в резистор со всех сторон, а из батареи э. д. с. — вытекают.

          2. Двухпроводная линия.

 

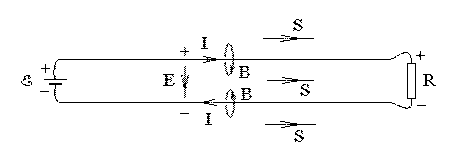
Энергия распространяется от э. д. с. к нагрузке рядом с проводами линии, а не по проводам.

          Есть два способа описания одной и той же энергии:

          1). Энергия зарядов, которая передается по проводам.

2). Энергия поля, которая проходит рядом с проводами.  Энергия зарядов — это потенциальная энергия W = qϕ.

Если рассматривать переменные поля, то поле не потенциально. Поэтому у зарядов нет энергии в обычном смысле. Остается только энергия поля.

Энергию зарядов можно рассматривать до тех пор, пока r <<λ, где r — размер электрической схемы. Так для частоты 50 Гц: λ= ^c =

ν

(300000 км/с) / (50 1/c) = 6000 км.

Рассмотрим источник переменного напряжения с частотой 50 Гц, который подсоединен к длинной двухпроводной линии. Пусть на удаленном конце двухпроводная линия короткозамкнута.

 

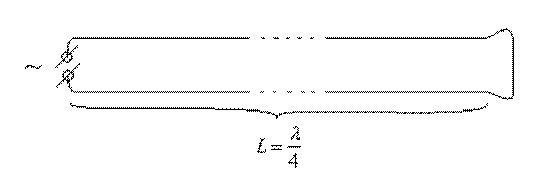
Пусть длина двухпроводной линии L =  = 1500 км. Оказывается, что короткое замыкание на удаленном конце линии будет восприниматься источником напряжения, как разрыв, а не как короткое замыкание.

Длина  эквивалентна сдвигу фаз . Пусть в какой-то момент времени потенциал верхней клеммы источника