Напряжение на выходе линейной схемы при произвольной зависимости напряжения на входе от времени (второй подход)

Факультатив. Напряжение на выходе линейной схемы при произвольной зависимости напряжения на входе от времени (второй подход).

        В математике есть операции прямого и обратного преобразования Фурье:

   ^R||S ~ 0a f +z∞ ~a f i             t

                       y ω = ¹ ⋅         y t ⋅e^−ωdt

2π −∞

        T| ~a f +z∞ ~ 0a f i      t

                |y t =        y ω ω⋅eωd

−_∞

         Применим прямое преобразование Фурье к напряжению на входе схемы:

~

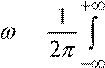           U0_вх ( ) =          Uвх ( )t ⋅e−i tωdt .

~

Здесь U0_ вх ( )ω ω⋅d — комплексная амплитуда входного напряжения в полосе частот от ω до ω+ dω, что видно из обратного преобразования Фурье:

+∞ _~

         Uвх ( )t = ∫ U0_вх ( )ω ω⋅ei tωd         .

−∞

Комплексная амплитуда напряжения на выходе схемы для каждой частоты сигнала выражается через комплексную амплитуду на входе и комплексный коэффициент передачи:

                ~                         ~               ~                              ~

U_{0_ вых} ( )ω = K_U ( )ω ⋅U_{0_вх} ( )ω , где K_U — комплексный коэффициент передачи по напряжению, который мы умеем находить. Сделаем соответствующую замену в обратном преобразовании Фурье для выходного напряжения:

+∞ _~

         Uвых ( )t = ∫ U0_вых ( )ω ω⋅ei tωd                       =>

−∞

                                        +∞ ~              ~

         Uвых ( )t = ∫ KU ( )ω ⋅U0_вх ( )ω ω⋅ei tωd 

−∞

          Тогда U~0_вх ω = 1 +∫∞U        t ⋅e−i tωdt

( ) π вх ( )

                                 2 −∞

           ( )t ⁼ +∫∞K~_U ( )ω ⋅U~_{0_вх} ( )ω ω⋅ei tωd      .

U_вых

                            −∞

         Эти два равенства позволяют найти напряжение на выходе схемы

U_вых (^t) через напряжение на ее входе U_вх (^t), если мы знаем комплексный

~

коэффициент передачи схемы K_U ( )ω , как функцию частоты ω.

Экзамен. Трансформатор.

(в системе СИ)

Трансформатор — две катушки на общем замкнутом сердечнике с высокой магнитной проницаемостью µ>>1.

 

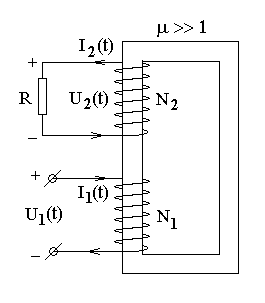
Чтобы правильно найти связи между величинами нужно внимательно следить за их знаками.

          Правило знаков.

1.  Пусть обе катушки намотаны в одну сторону и расположены на одной стороне сердечника.

2.  U₁ > 0, если на верхнем проводе "+" напряжения.

3.  U₂ > 0, если на верхнем проводе "+" напряжения.

4.  I₁ > 0, если ток через катушку течет сверху вниз.

5.  I₂ > 0, если наоборот, ток через катушку течет снизу вверх.

Дело в том, что при этом ток через сопротивление R течет сверху вниз и U₂ = RI₂ . Иначе было бы U₂ = −RI₂ .

           Обозначим за Φ поток поля B через один виток.

                 E          = − d N( 1Φ)

инд_1

                                       dt

                E           = − d N( ₂Φ)

                инд_2              dt

U1 + Eинд_1 = 0

         ^^U₂ + E_{инд_2} = 0                              (1)               =>

Φ = BS



B =µµ0 H

Hl = N I11 − N I2 2

U₂ = RI₂

Из средней четверки системы из восьми уравнений выразим четыре неизвестных

 Eинд_1 = −U1



Eинд_2 = −U2

                       и подставим их в остальные уравнения. Тогда получим

B =µµ0 H

^Φ = S ⋅µµ₀ H

систему из четырех уравнений

              R           •

|U₁ = N S₁ µµ₀             H |^|S     •

          U₂ = N S₂ µµ₀            H                  (2) |

        T||Hl = N I1 1 − N I2           2

U₂ = RI₂

          Разделим второе уравнение системы (2) на первое и получим

           U^{2 = N2}                 <=>              U₂ ^{= N2} U₁            <=>       U₂ = nU₁ ,                где

                U1        N1                                                                   N1

n ^{≡ N2} — коэффициент трансформации. N₁

           Решения для неизвестных величин будем подчеркивать U =     ²

                                                                                                                                                                                   U N

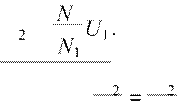           Напряжение в каждой обмотке пропорционально числу витков  

U1 N1 при любой зависимости U t₁a f.

Однако на опыте, если U₁ = const , то U₂ = 0. Причина в том, что мы не учли активное сопротивление первичной обмотки. В стационарном случае, каким бы малым ни было сопротивление первичной обмотки, постоянное напряжение выделяется именно на нем, а не на индуктивности, поэтому напряжение не переходит во вторичную обмотку.

      В четвертое уравнение U₂ = RI₂ системы (2) подставим U₂ ^{= N2} U₁ и

N₁ получим

  I2 = N2 ⋅U1 . N₁ R

•

          Из     первого     уравнения      U₁ = N S₁ µµ₀ H      системы     (2)      выразим напряженность магнитного поля в сердечнике и получим

           H=       ¹  zt U t dt₁a f'         '.

µµ0 N S1 −∞

Из третьего уравнения U₁ + E_{инд_1} = 0 системы (1) получим  Eинд _1 = −U1.

          Из четвертого уравнения U₂ + E_{инд_ 2} = 0 системы (1) получим

          Eинд_ 2 = −U2 = − N2 U1                   =>

N₁

          Eинд_ 2 = − N2 U1

N₁

           Из шестого уравнения B = µ₀µH системы (1) получим

          B = µµ₀ H = ¹ z_t U t dt₁a f'      '         =>

N S₁ −∞

1  zt               a f

          B =           U t dt₁ ' '

N S₁ −∞

           Из пятого уравнения Φ= BS системы (1) получим

    Φ = BS = ¹ z_t U t dt₁a f'        ' =>

N1 −∞

t

          Φ = ¹U t dt₁a f' '

N1 −∞

          Из седьмого уравнения Hl = N I_{1 1} − N I_{2 2} системы (1) получим

FGH    IJK 2             zt       a f FI 2   t

            I1 = N2 I2 + Hl =    N2      U1 + µµ0 lSN12 −∞U t dt1 ' '                   =>

                           N1             N1           N1         R

        I1 =HN2 JK U1 +     l 2 zU t dt1a f'          '

                              N₁            R µµ0 SN1 −∞

          Проанализируем эту формулу при R → ∞         =>

    I₁ ⁼ µµ0 lSN1₂ −zt∞U t dt₁a f'                     '            => U₁ µµ0 lN S12 • = L I11 •1                                    =>

                                                                                                               =                I1

                         =µµ0 N S12      =>

           L11

l

      I₁ = _F^U1I + ¹ zt U t dt₁a f'     ',

R   L11 −∞ Hn2 K

                       где n = ^N2 — коэффициент трансформации. N₁

Условие R → ∞ — это условие отсутствия нагрузки во вторичной обмотке трансформатора. Ток первичной обмотки при этом называется холостым током трансформатора. Для уменьшения холостого тока нужно стремиться увеличить индуктивность первичной обмотки L₁₁ → ∞, при этом

I1 = FU1I .

R

Hn2 K

R

Тогда можно сказать, что величина ₂ — это сопротивление нагрузки