Магнитное поле внутри бесконечного соленоида. Магнитное поле на оси соленоида конечной длины. Магнитное поле над токонесущей плоскостью

Внутри бесконечного соленоида Ω = 4π — полный телесный угол (телесный угол вовсе стороны), так как куда ни посмотришь из точки наблюдения поля, взгляд упирается в поверхность с током.

          Тогда

B = 4^{πi = 4}πnI — поле внутри бесконечного соленоида, где i — c    c

плотность поверхностного тока соленоида, n — число витков на единицу длины соленоида, I — сила тока в одном витке соленоида.

Факультатив. Магнитное поле на оси соленоида конечной длины.

Найдем магнитное поле в точке O на оси соленоида с поверхностной плотностью тока i = nI , где n — число витков на единице длины соленоида, I — сила тока в одном витке.

 

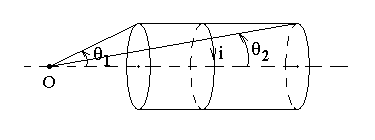
Здесь θ₁ и θ₂ — угловые радиусы донышек цилиндра при взгляде из точки наблюдения магнитного поля.

Ось соленоида является поворотной осью симметрии задачи. Решение должно обладать этой же симметрией. Тогда на оси симметрии может быть только осевая составляющая магнитного поля.

Для любого элемента поверхностного тока составляющая B_⊥ направлена вдоль оси соленоида. Тогда поле на оси:

                          B = B_⊥ = ⁱ Ω = ^Ω nI c   c

Найдем телесный угол Ω, под которым видна поверхность с током из точки наблюдения магнитного поля.  dΩ = _sina^θf⋅dθ⋅dϕ =>

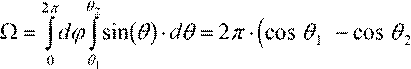          b g b   gh Ω          ^2π c b ₁g    b ₂ gh

                            Тогда B =     nI =   nI ⋅ _cosθ − _cosθ c         c

B ^{= 2π}nI ^⋅c_cosbθ₁g− _cosbθ₂ gh — поле на оси соленоида, где n — число c

витков на единицу длины соленоида, I — сила тока в соленоиде, θ₁ и θ₂ — угловые радиусы торцов соленоида при взгляде из точки наблюдения поля.

1 µ⁰

          В системе СИ:  →      .

                                                      c      4π

Факультатив. Магнитное поле над токонесущей плоскостью.  Магнитное поле закручено вокруг токов по правилу правого винта. В таком случае магнитное поле плоскости с током имеет следующий вид:

 

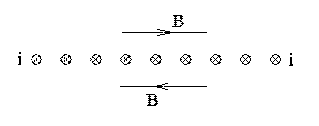
Это поле перпендикулярно току и параллельно поверхности с током. i

Тогда магнитное поле можно найти по формуле dB . Телесный угол, под которым видна бесконечная плоскость с током, равен 2π. Тогда

B ^{= 2}πi , где поле B закручено вокруг тока по правилу правого винта, c

поле параллельно токонесущей плоскости и перпендикулярно току.

Экзамен. Векторный потенциал.

    dA ^{≡ I ⋅ dl} — векторный потенциал элемента тока I ⋅dl на расстоянии r

                            c    r

от элемента тока.

µ dl

          В системе СИ: dA          I .

r

                                       Выражение dA ≡ ^I ⋅ ^dl похоже на выражение ϕ= ^q , где ϕ — скалярный c        r         r

потенциал. Поэтому      A        называют    векторным потенциалом, хотя   к потенциальной энергии он не имеет никакого отношения.

FϕI GG A_x^JJ GGH AyJJK

           Интересно, что         — 4-х вектор относительно преобразований

A_z

FctI

G_xJJ GGH yJJK

Лоренца, так же как .

z

          Рассмотрим rot dAc   h:     rot dAc h = LNM∇, I ⋅ dl OQP = I ⋅ ∇LNM ,1dl OQP = I ⋅ ∇LMN 1,dl OPQ. c  r         c        r c        r

ϕ= q_r



           Подставим сюда ∇¹r = − r^r₃ , что следует из E = q r^r₃ , и получим

E = −∇ϕ



                          rot dAc h = I ⋅ ∇NLM 1,dl QOP = I ⋅ −LNM r3 ,dl QOP = I ⋅LNMdl , r3 QOP = I ⋅ dl r3, c       r         c        r    c        r         c        r

          Сравним этот результат с законом Био-Савара dB = ^I ⋅ dl r₃,      и получим:

                                                                                                                                                  c      r

         rot dAc h = dB   =>

  B = rot Ac h— связь магнитного поля B и векторного потенциала A.

      dA ≡                   =>

                            c    r

   A ra f = z 1⋅ j ra 'f ⋅dV'

Факультатив. Потенциалы переменных электромагнитных полей.

R^||^|S q t^FH − ^rIK ϕat r, f = ^c

r

           T^|| a f I tFH − rIK ⋅dl

                   dA t r,  =          c

cr

      Потенциалы зависят от зарядов и токов в предшествующий момент

r времени. Момент времени предшествует на время распространения сигнала  c от источника до точки наблюдения.

          Точнее и подробнее этот вопрос будет рассмотрен в конце курса.

Факультатив. Дивергенция векторного потенциала.

      div Ac h = 0

Это равенство справедливо только для постоянных токов. Формулу нужно знать на экзамене. Доказательство формулы на экзамене знать не нужно.  Это равенство можно доказать только для замкнутых токов. Постоянные токи замкнуты.

Сначала рассмотрим дивергенцию векторного потенциала для элемента тока, а не для замкнутого контура с током.

div dAc    h = FGH∇, I ⋅ dl IJK = I ⋅ ∇FH ,1dl IK = I ⋅ ∇FH 1,dl IK c       r         c        r        c        r

ϕ= q_r



           Подставим сюда ∇¹r = − r^r₃ , что следует из E = q r^r₃ , и получим

E = −∇ϕ



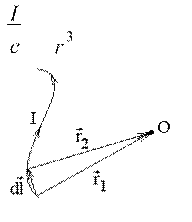         div dAc h = I ⋅ −FH r3 ,dl IK = −      ⋅dr dl,        i

                                        c       r

          Из рисунка видно, что

          r₁ = dl + r₂            => dl ^{= −}br₂ − r₁g = −dr

         Подставим это в выражение для div dAc h и получим

         div dAc h = ^I ⋅ a^{r dr,} ₃ f

                                        c      r

Рассмотрим