Реакция схемы на ступеньку напряжения на функцию Хевисайда. Реакция RC-цепочки на ступеньку напряжения

Экзамен. Реакция схемы на ступеньку напряжения.

(на функцию Хевисайда)

Постановка задачи. Внешний источник подает на схему ступеньку напряжения в нулевой момент времени. Найти токи и напряжения на элементах схемы, как функции времени.

          Этапы решения задачи:

1.  Внешний источник напряжения рассмотрим, как э. д. с., зависящую от времени.

2.  Напишем уравнения Кирхгофа 1-го и 2-го рода, которые окажутся дифференциальными уравнениями для токов.

3.  Исключая переменные, перейдем от системы уравнений к одному уравнению более высокого порядка.

4.  Решим это уравнение, а затем через его решение найдем все токи.

5.  Произвольные константы интегрирования обычно можно найти из условий:

Ua0f = 0 для каждого конденсатора, так как заряд конденсатора в нулевой момент времени не может измениться скачком. Такое изменение означало бы бесконечную силу тока.

Ia0f = 0 для каждой катушки индуктивности, так как ток катушки в нулевой момент времени не может измениться скачком. Такое изменение тока означало бы бесконечное напряжение на катушке.

6.  Зная токи, найдем напряжения на всех элементах схемы.

Экзамен. Пример 1. Реакция RC-цепочки на ступеньку напряжения.

 

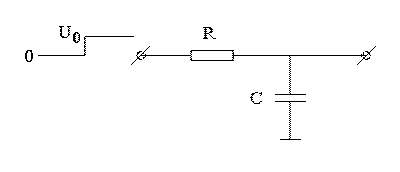
Пусть резистор и конденсатор включены последовательно. На эту схему в нулевой момент времени подают ступеньку напряжения величиной U₀ . Нужно найти напряжение на конденсаторе, как функцию времени.

 Та же самая схема была рассмотрена в вопросе "Интегрирующая RCцепочка", но в том вопросе было дополнительное условие U_вых(^t) << U_вх(^t) , которое в данном вопросе не выполнено. Зато вместо произвольной функции времени на входе схемы может быть только ступенька напряжения.

--------

          Напомним уравнения Кирхгофа.

           1). ∑E_i ⁼ ∑U_i — для любого контура.

                          i                 i

           2). ∑I_i = 0 — для любого узла.

i

--------

          Рассмотрим       уравнение ∑E_i ⁼ ∑U_i        для     единственного              контура.

                                                                                      i                 i

Напряжение на входе можно рассматривать, как внешнюю э. д. с.

          После     включения     ступеньки     напряжения     выполнено         условие:

U₀ = RI + ^q , которое можно переписать в виде дифференциального уравнения

C

•

относительно заряда q на конденсаторе с учетом того, что I = q:

                                 •      q

           U₀ = Rq+          =>

C

•+ 1 q = U0  q

                        RC        R

Общее решение этого неоднородного уравнения равно сумме частного решения неоднородного уравнения и общего решения однородного уравнения.  Найдем частное решение неоднородного уравнения в виде константы.

          q = const     =>     q• = 0           =>        1 q = U0             => q = CU0                 —

                                                                                                         RC        R

частное решение дифференциального уравнения.

          Найдем теперь общее решение однородного уравнения

                •        1

          q+ q = 0.

RC

          Факультативная математическая вставка.

Линейное дифференциальное уравнение n -го порядка с постоянными коэффициентами имеет следующий вид:  a y_n aⁿf + a_n−1yaⁿ⁻¹f+ +... a y a y₁ '+ ₀ = 0.  Общее решение этого уравнения имеет вид:

_{y t}a f = Ae₁ ^λ1t + A e₂ ^λ2t + +... A e_n ^λnt , A_i — произвольные константы интегрирования, λ_i — решения характеристического уравнения, которое получается при подстановке в уравнение решения в виде y = Ae^λt .

Подставим и после сокращения каждого слагаемого на Ae^λt получим:    a_nλ λⁿ + a_n−1 ⁿ⁻¹+ +... a₁λ+ a₀ = 0 — характеристическое уравнение.

          Конец факультативной вставки.

•+ 1 q = 0 подставим q = Aeλt и получим  В нашем случае в уравнение q

RC

 d dAe^λt i+ ¹ dAe^λt i = 0 => λ+ ¹ = 0  => λ= − ¹ . dt RC RC RC

                                                                                                                                     •         1

          Тогда общее решение однородного уравнения q+ q = 0 имеет вид

RC

− t

           q = Ae ^RC .

•+ 1 q = U0 имеет вид  Общее решение неоднородного уравнения