Закон Ампера и сила Ампера. Элемент тока. Закон Био-Савара (Лапласа). Формула для расчета магнитного поля B в плоской задаче

Экзамен. Закон Ампера и сила Ампера.

                   dF = ^I ⋅ dl B, — сила Ампера, действующая на элемент тока I ⋅dl . c

           В системе СИ: dF = I ⋅ dl B,   = µ₀I ⋅dl H, .

           B — магнитная индукция или просто магнитное поле.

Усредненное микроскопическое магнитное поле среды называют магнитным полем B в среде. В этом смысле B — истинное магнитное поле.

H — напряженность магнитного поля — вспомогательная величина, которая будет введена в рассмотрение позднее.

          В вакууме: B = H .

          В СИ: B = µ₀H .

1

Факультатив. . c

При рассмотрении магнитных полей в системе СГС Гаусса сила тока I , плотность тока j , плотность поверхностного тока i всегда входят в формулы с

1

коэффициентом   . Причина этого в том, что ток пропорционален скорости c

движения зарядов.

          Рассмотрим объем dV₀ = Vdt S⋅        , где V — скорость движения зарядов.

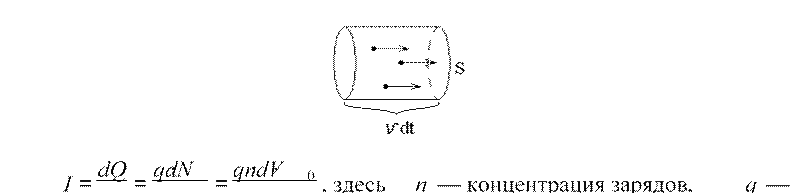
                          dt        dt             dt

величина каждого заряда.

I = ^{q n dV}⋅ ⋅ ⁰ = ^qn⋅ ^{Vdt S}⋅      = nq SV       =>         j = ^I = nqV         => dt  dt       S

            j = nq V ,

 где j — плотность тока, n — концентрация зарядов, q — величина каждого заряда, V — средняя скорость зарядов.

Любой физический эффект, пропорциональный току пропорционален и скорости зарядов.

V

 — безразмерная скорость, поэтому в формулах с токами появляется c

1

коэффициент  .

c

Кроме         того, магнитные эффекты     могут          быть объяснены, как релятивистские поправки к электрическим эффектам.

Факультатив. Элемент тока.

1).	j =  => dI = j dS⋅ ⊥. Подставим это выражение для тока в dS⊥
	Idl = j dS⋅ ⊥ ⋅dl = j dS⋅ ⊥ ⋅dl = jdV .
2).	i = dI => dI = i dl⋅ ⊥ . Подставим это выражение для тока в dl⊥
	Idl = Idl|| = i dl⋅ ⊥ ⋅dl|| = i dl dl⋅ ⊥ || = idS .
3).	Idl = dQ ⋅dl = dl ⋅dQ. Приравняем два выражения для величины

Получим различные выражения для элемента тока Idl . ^dI

                                              dt            dt

dl . Одно dl такое, на котором находится заряд dQ. Другое dl — перемещение

dl

зарядов тока за время dt . Тогда  = V             =>

dt

                  Idl ^{= dl} dQ = VdQ = qV .

dt

          Объединяя разные выражения для элемента тока, получим

           I dl⋅   ↔ j dV⋅   ↔ i dS⋅   ↔ qV — элемент тока в разных формах.

--------

Вернемся к рассмотрению силы Ампера, которая пропорциональна элементу тока.

           dF = ^I ⋅ dl B,      =>

c

          Другие формы силы Ампера:

 dF = ¹⋅ j B, ⋅dV => dF = ¹⋅ i B, ⋅dS  => c    c

       F ^{= q}c ⋅^V,B^ — сила Лоренца.

Строго говоря, выражение для силы Лоренца не следует из закона Ампера, так как в нем рассматриваются силы, действующие на постоянные токи. Однако, как показывает опыт, выражение для силы, действующей на движущийся заряд, именно такое.

          Иногда силу Лоренца определяют иначе: F = qE ^{+ q} ⋅^V,B^ . _c   В системе СИ: F = q⋅^V,B^ =^µ₀q⋅^V,H^

Экзамен. Закон Био-Савара (-Лапласа).

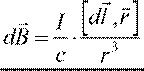                     — поле элемента тока I ⋅dl , где r — вектор, направленный из элемента тока в точку наблюдения.         Другие формы закона Био-Савара:

                            1    j r,

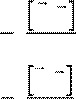 dB = ⋅ ₃ ⋅dV c r

                            1    i r,

dB = ⋅ ₃ ⋅dS c r

_q [V,r]

          B = ⋅  — магнитное поле заряда q , движущегося с постоянной

                          c      r3

скоростью V .

Строго говоря, формула для магнитного поля движущегося заряда не следует из закона Био-Савара, так как закон Био-Савара относится только к постоянным токам. Однако, как показывает опыт, магнитное поле движущегося заряда именно такое.

µ dl r,           В системе СИ: dB =    0 I ⋅      3      , 4π r

dH = 1πI ⋅ dl rr3, 4

Факультатив. Формула для расчета магнитного поля B в плоской задаче.  Плоская задача — все токи и точка наблюдения поля B находятся в одной плоскости. В таком случае в плоскости задачи находятся векторы dl и r

                                                                       I    dl r,

в законе Био-Савара dB =       ^⋅     ₃                  . Вектор dB перпендикулярен плоскости

                                                                       c      r

задачи, как векторное произведение двух векторов в этой плоскости.

Следовательно, все вклады dB в магнитное поле параллельны друг другу, и их можно складывать, как числа, а не как векторы.

I       dl r, c r

            В формуле для магнитного поля dB =     ^⋅     ₃   заменим r → −r . Тогда новый вектор r направлен из точки наблюдения к элементу тока, r — радиусвектор элемента тока, если считать, что начало координат расположено в точке наблюдения магнитного поля.

                                                                         I    r dl,

          Для нового r :      dB =   ⋅      ₃      .     =>

                                                                         c      r

                   dB = I ⋅ r dl⋅ ⋅sin3 aθf = I ⋅ dl ⋅sin2 aθf . c       r         c r

Здесь θ — угол между векторами r и dl . Пусть O — точка наблюдения магнитного поля, тогда

 

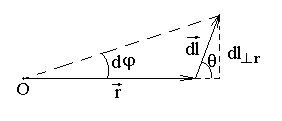
Отрезок dl_⊥r можно выразить двумя способами. С одной стороны  dl_⊥r = dl ⋅sina^θf,  а с другой стороны  dl_⊥r = r d⋅ ϕ.

          Тогда

        dl ⋅sina^θf = r d⋅ ϕ

       Подставим это в выражение dB = ^I ⋅ ^{dl ⋅sin}₂ a_θf и получим

                                                                                                    c        r

           dB = I ⋅ dϕ,

                      где dϕ — угол, под которым элемент тока виден из точки наблюдения; r

— расстояние от точки наблюдения до элемента тока; dB — вклад элемента тока в магнитное поле в точке наблюдения.

          Эта формула полезна для решения задач.

Факультатив. Магнитное поле в центре кругового витка с током.     Все токи и точка наблюдения находятся в одной плоскости. Тогда           dB = I ⋅ dϕ         => c   r

                 B = zdB = z I dϕ= I ⋅zdϕ π= I ⋅2          = 2πI    => _{l      l} cr      cr _l    cr       cr

          B = 2π⋅ I

cr

                                                          1 µ⁰                                               µ^0I

В системе СИ:       →             =>      B =    . c      4π    2r

Экзамен. Магнитное поле прямого провода с током.

Рассмотрим прямой провод с током и одну точку наблюдения магнитного поля. Через прямую и точку вне нее проходит плоскость. Следовательно, задача плоская и можно воспользоваться формулой  dB = I ⋅ dϕ.

                             c    r

      На экзамене этой формулой можно воспользоваться, как исходной.

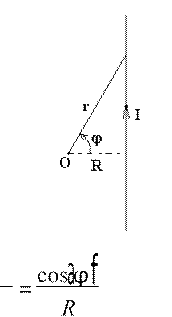
           R = cosaϕf     =>      ¹         r        r

Подставим это выражение для 1 в выражение dB = ^I ⋅ ^dϕ и получим