Экзамен. Экранирование электростатического поля проводником.
Переменное электромагнитное поле тоже экранируется, но не полностью.
Если в проводнике есть полость без зарядов, то внутри полости E= 0 независимо от того, есть ли заряды снаружи проводника.
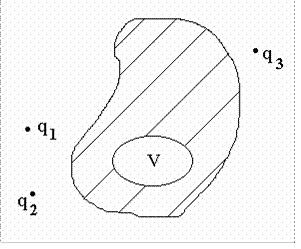
Рассмотрим объем полости V внутри тела проводника. Граница S объема V эквипотенциальна, так как является поверхностью проводника. Пусть потенциал этой поверхности равен ϕ0. Тогда ϕ ϕS = 0.
![]() Придумаем
в объеме V решение для уравнения ∆ϕ=−4πρ.
Придумаем решение в виде постоянного потенциала ϕarfV=ϕ0.
Придумаем
в объеме V решение для уравнения ∆ϕ=−4πρ.
Придумаем решение в виде постоянного потенциала ϕarfV=ϕ0.
![]() Это решение удовлетворяет
условию краевой задачи Дирихле ϕ ϕS=
0.
Это решение удовлетворяет
условию краевой задачи Дирихле ϕ ϕS=
0.
Это решение удовлетворяет и уравнению ∆ϕ=−4πρ в объеме V , так как в этом объеме нет зарядов: ρ= 0 , и так как производные от постоянного потенциала ϕ0 равны нулю: ∆ϕ= 0 .
Из единственности решения краевой задачи Дирихле следует, что другого решения для потенциала в полости быть не может. Значит, придуманное нами решение для потенциала в объеме полости V и будет настоящим решением для потенциала в полости.
ϕarf![]() V= =ϕ0 const
=> E=
0
V= =ϕ0 const
=> E=
0
Внутри полости поле E отсутствует или, что то же самое, проводник экранирует электростатическое поле.
Факультатив. Заряд внутри полости проводника.
Рассмотрим задачу: пусть есть незаряженный проводящий шар, внутри шара — сферическая полость, в центре полости точечный заряд. Найти поле E везде.
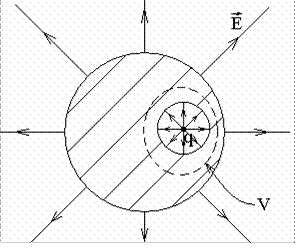
Сначала докажем, что на внутренней поверхности проводника, на поверхности полости, соберется заряд −q. Для этого применим теорему Гаусса к пунктирной границе S объема V . Все точки поверхности S находятся внутри объема проводника. Следовательно, в точках границы S отсутствует поле E . Тогда и поток поля E через поверхность S равен нулю: ΦE = 0. С учетом теоремы Гаусса ΦE = 4πQ. Тогда Q = 0, сумма зарядов внутри поверхности S равна нулю. Внутри объема проводника зарядов нет. Следовательно, если в полости заряд q , то на границе полости находится заряд −q.
Проводник не заряжен. Если на поверхности полости находится заряд −q, то на внешней поверхности проводника должен быть суммарный заряд q .
Теперь можно решать две совершенно независимые задачи.
В 1-ой задаче рассмотрим объем полости V . В этой задаче в центре объема V находится точечный заряд
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.