Дополнение к теореме Лармора. Гиромагнитное отношение. Спин электрона. Диамагнетизм

Факультатив. Дополнение к теореме Лармора.

         Мы доказали, что в магнитном поле электронная оболочка может вращаться с частотой Ω= ^e B. 2mc_e

           Однако будет ли она раскручиваться при включении магнитного поля?

          Оказывается, что будет.

Дело в том, что при включении магнитного поля вокруг его производной по времени возникает вихревое электрическое поле, которое и раскручивает электронную оболочку.

       Для доказательства достаточно доказать, что в системе K', которая вращается с переменной угловой скоростью Ω= ^e         B , сила со стороны 2m c_e

вихревого электрического поля F = qE уравновешивается силой инерции, которая возникает при ускоренном вращении системы K'.

                                         •                  e       •           e  •         e  • 

          F_ин =−m_eΩ,r =−m_e B r, =− B r, = r B, 

                                                2m ce      2c    2c   

                 Найдем величину E вихревого электрического поля, которое возникает

∂B вокруг           производной от магнитного поля.

∂t

 

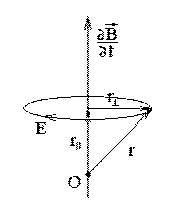
          Здесь O — центр атома — атомное ядро, r — радиус-вектор электрона, ∂B

r_|| — составляющая радиус-вектора электрона вдоль производной    , r_⊥ —

∂t

∂B

составляющая радиус-вектора электрона перпендикулярная производной                                                                                                .

∂t

     Вихревое электрическое поле можно найти из уравнения Максвелла

rot Ec h = −¹ ∂^B ,     которое       в        интегральной       форме    совпадает    с        законом c ∂t

электромагнитной индукции Фарадея:

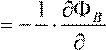 E dl_l, где    контур         интегрирования   —      окружность, lc      t

                                                                                  ∂B      ^•

перпендикулярная производной         = B.

∂t

                                                          1 ∂ d  ² i                ^{r⊥   •}

Тогда 2πr E_⊥          = −     ^⋅ πr B_⊥                      =>      E = −         B        => c ∂t        2c

Как видно из рисунка, направление вихревого векторного поля E L   ^•O

совпадает с направлением векторного произведения _NMr B_⊥, _QP, тогда с учетом

E = − ^r⊥ B^• получим

2c L ^•O

  E = ¹ NMr B_⊥, QP.

2c

Сила, действующая на электрон с зарядом q = −e со стороны вихревого электрического поля равна

L ^•O e M QP

          F = qE = −eE = −      r B_⊥,  .

2c N

Сравним эту силу с силой инерции ускоренно вращающейся системы отсчета

                                e     •      e             •      e     •      e       •      e       • 

           F_ин = r B,  = r_|| + r⊥,B = r B_||,         +   r⊥,B =      r⊥,B,

                            2c     2c             2c     2c      2c    

        L • O            •

где NMr B_||, _QP= 0, так как r B_|| ||      . Тогда

          F + F_ин = 0 — дополнение к теореме Лармора доказано.

Экзамен. Гиромагнитное отношение.

Гиромагнитное отношение — отношение магнитного момента электрона к его механическому моменту импульса.

------

Рассмотрим сначала отношение магнитного момента к механическому моменту импульса при движении электрона по окружности вокруг ядра атома.  Момент импульса:

      L = ^r m V, _e ^    =>     L = rm V_e .

          Теперь найдем магнитный момент.

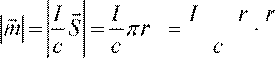                                    2 = I ⋅2πr r⋅

                                                                     c       2

Разделим магнитный момент на механический и получим гиромагнитное отношение

m         I ⋅πr² I ⋅2πr          γ =    = =       .

                            L     c rm V⋅         e  2m cVe

Подставим в правую часть равенства 2πr =VT , где длина пути равна произведению скорости на время, T — период обращения электрона. Тогда

                γ =   IT   =    e    ,

                          2m c_e    2m c_e

  где последнее равенство получено с учетом I ^{= e} — сила тока равна

T

отношению заряда ко времени его прохождения через сечение проводника (в нашем случае, через сечение орбиты электрона).

          Момент импульса L образует правый винт с направлением движения электрона по орбите. Заряд электрона отрицательный, поэтому магнитный момент образует левый винт с направлением движения электрона по орбите.        Следовательно,  γ= −   ^e .

2m c_e

------

Найдем теперь гиромагнитное отношение в более общем случае и покажем, что оно такое же и в общем случае.

Рассмотрим момент импульса электрона при его движении вокруг ядра атома не обязательно по круговой орбите.

          L = r mV, e = me r dr, 

dt

Проведем усреднение этого выражения по замкнутой орбите движения электрона. Тогда

z r dr,

                 L = m_e ^l.

T

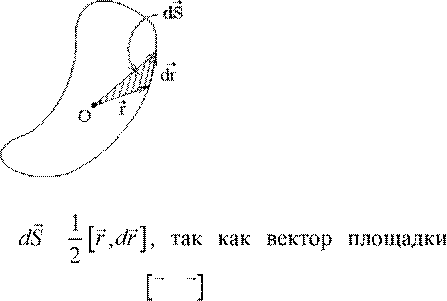             Из рисунка видно, что dS =           , так как вектор площадки dS

направлен, как и векторное произведение r dr,     , а длина вектора dS = dS

равна площади заштрихованного треугольника dS = ¹ ⋅ ⋅r dr ⋅sina∠r dr,                                                                                                        f, что

2

совпадает с половиной длины векторного произведения