Формализованное описание процесса синтеза системы сбора и анализа социально-психологической информации о состояниях воинских коллективов, страница 4

     б)U_n(X_G⁰,Х_П⁰) ® min;                       (2.17)

при условиях 

U_n (X_G⁰,Х_П⁰) £ U_n^*;

S(X_G⁰,Х_П⁰) £ S_доп

С  учетом  формулы  (2.12)  задача  рационального выбора структуры и состава системы АСАСПИ может быть сформулирована следующим  образом.  Необходимо  найти такие подмножества X_G⁰ и Х_П⁰ (X_G⁰ÍX_G ,Х_П⁰ÍX_П),  при которых выполняются ограничения (2.13)  и (2.14), а функционал будет минимальным, т.е.   

       F(S,U_n)® min;                    (2.18)                                         

при условиях   U_n(X_G⁰,Х_П⁰) £ U_n^* ;

               S(X_G⁰,Х_П⁰) £ S_доп

Строгое решение задачи (2.18) в общем виде представляет значительные  трудности, связанные с установлением достаточно простых и удобных зависимостей, связывающих показатели качества S(·) и U_n(·) с параметрами оптимизации Х_п, Х_с.  В большинстве  случаев  функции S(·) и U_n(·) имеют нелинейный характер, и задача (2.18) сводится к задаче целочисленного нелинейного программирования. Задачи данного класса характеризуются громоздкостью вычислений и отсутствием единой методологии их решения [17, 22].

Поэтому предлагается поэтапное (многошаговое) решение задачи синтеза рациональной (квазиоптимальной) структуры и состава АСАСПИ.

Алгоритм решения задачи синтеза АСАСПИ определяется последовательностью ряда шагов (см. рис.2.3).

ШАГ 1. Ввод исходных данных.

Осуществляется ввод структурных параметров системы и характеристик задач, определенных в разделе 2.2.

ШАГ 2. Оценка параметров существующей системы.

Задача оценки параметров АСАСПИ заключается в определении требуемых значений быстродействия (пропускной способности) элементов системы, типов и количества однотипных устройств на рабочих местах пользователей, времени пребывания в системе задач пользователей, а также стоимости существующей системы.

ШАГ 3. Проверка соответствия параметров системы требуемым значениям в соответствии с выражениями

              r_ij < 1                           (2.19)                                                                        

              k_ij^min < k_ij                       (2.20)                                                                  

              U_n £ U_n^*                              (2.21)

Данные выражения являются условиями перехода к проверке допустимого решения для заданного варианта структуры и состава АСАСПИ. При выполнении данных условий принимается решение о соответствии с существующей СОИ предъявляемым требованиям, производится переход к шагу 9.

При невыполнении хотя бы одного условия существующая система не обеспечивает качественного решения задач, требуется изменение значений параметров V, V_к, k_i отдельных элементов системы или изменения структуры системы в целом.

ШАГ 4. Проверка существования допустимого решения для заданного варианта структуры АСАСПИ из множества X_G.

Для каждого варианта X_G⁰ из множества X_G выполняется проверка существования допустимого решения, которая сводится к последовательности следующих этапов:

Этап 1. Для всех элементов системы   задаются максимально возможные значения параметров:

V_к = V_max^l1; V=V_max^l2;k=W_подр;

 Этап 2. Вызов процедуры оценки параметров системы и расчет времени пребывания в системе задач социально-психологического обеспечения.

При первом обращении к указанной процедуре заданным вариантом структуры АСАСПИ является существующая в учреждении (части) структура СОИ. При последующих обращениях задается очередной вариант из множества X_G.

ШАГ 5. Проверка ограничения (2.21).

При невыполнении заданного ограничения выбирается новый вариант структуры системы из множества X_G и осуществляется переход к этапу 1, иначе – переход к шагу 6.

ШАГ 6. Расчет параметров элементов АСАСПИ с заданным вариантом структуры.

Этап 1. Расчет параметров потоков заявок и параметров задач  с учетом задач социально-психологического обеспечения:

            L_nj=l_nj + l_njспо;

                  L_0j=L_nJ;

             n₁    n₁                           

          q_j=å q_ij + å q_ijспо ;                  (2.22)                                                                                  

             i=1  i=1                                                             

           N_ву= N_ву +  N_{ву спо};

            a₁ = N_вуi+1;

            a_i,j = N_вуij;

            a_k = N_вуi

            l_nij= a_ij´L_n;

            l_ij=l_nij;

            q_1j=q_j/a₁;

 ЭТАП 2. Выбор режима обработки социально-психологической информации:

режим пакетной обработки информации;

режим оперативной обработки информации;

Выбор режима обработки информации осуществляется оператором исходя из специфики задачи.

ЭТАП  3. Расчет оптимальных значений параметров элементов системы и формирование вектора S_q (X_G, X_П).

ШАГ 7. Проверка условия  q = Q, q = .

При q < Q выполняется операция q = q +1 и осуществляется переход к шагу 3.

При q = Q ( выбраны все варианты структуры АСАСПИ) осуществляется переход к шагу 8.

ШАГ 8. Выбор варианта структуры и состава АСАСПИ в соответствии с выражением (2.15).

ШАГ 9. Выдача результатов:

  1)Параметры синтезируемой системы :

Множества: А^спи,А^спи_n,А^спи_n+1,j,H;

Матрицы: B,C,D,E,Z;

    2)Параметры элементов системы:

k_ij,r_ij,U_n,m_j,S_спи.

Представленный алгоритм позволяет определить рациональный по критерию минимума стоимости вариант структуры и состава системы сбора и анализа социально-психологической информации о состояниях воинских коллективов при ограничении на время пребывания задач в системе на основе решения задачи оптимизации.

2.4. Процедура распределения производительностей элементов однопрограммных   систем  пакетной обработки  социально-психологической информации

Автоматизированная система  сбора и анализа социально-психологической информации функционирует в однопрограммном режиме, если в каждый момент времени все ресурсы предоставляются лишь одной задаче. Расчет оптимальных значений параметров элементов АСАСПИ заданной стоимости для однопрограммного режима пакетной обработки информации заключается в последовательном выполнении следующих действий.

ЭТАП 1. Расчет стоимостных коэффициентов для отдельных устройств

            k_j=k_jq_ij;                      (2.23)

ЭТАП 2. Расчет оптимальных значений интенсивности обслуживания заявок j-м пунктом размещения ПЭВМ

         m_i⁰=L_0j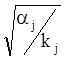 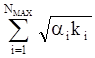;               (2.24)

ЭТАП  3. Расчет значений производительности элементов системы V_j

             V_j=m_j⁰q_ij;

ЭТАП 4. Присвоение V_j ближайшего большего дискретного значения из множества {V}.

ЭТАП 5. Расчет значения интенсивности обслуживания заявок

             m_j=V_j/q_j;