Формализованное описание процесса синтеза системы сбора и анализа социально-психологической информации о состояниях воинских коллективов, страница 3

Элементам системы сбора и анализа социально-психологической информации ставится в соответствие набор параметров (V, V_k, k) из множества возможных значений параметров Х_П, где

V – производительность процессора;

V_k – пропускная способность канала;

K – количество однотипных  устройств.

Стоимостные затраты на создание и эксплуатацию j-го элемента системы обработки информации, согласно [25], определяются выражением:

               S_j=k_iV_i+K_is_i..                       (2.8)

Переменная V_i в выражении (2.8) обозначает производительность процессора, если j-й элемент системы-ПЭВМ, или пропускную способность канала, если j-й элемент системы - канал связи. Суммарные затраты на систему из N элементов определяются выражением:

                   S=S_j.                       (2.9)             

При расчете стоимости затрат на создание и эксплуатацию АСАСПИ необходимо учитывать следующие факторы:

1) структуру и состав существующей в учреждении (части) системы обработки информации;

2) стоимостные затраты на создание и эксплуатацию системы с учетом задач социально-психологического обеспечения.

        В соответствии с указанными факторами будем полагать, что основу стоимостных затрат на создание и эксплуатацию системы АСАСПИ составляют затраты, связанные с модернизацией или приобретением, наладкой и установкой каналов связи ПЭВМ, периферийного и вспомогательного оборудования, необходимого для решения задач СПО, а также затраты на хранение прикладного программного обеспечения, нормативно-справочной и статистической информации о СПС воинских коллективов.

Введем следующие обозначения:

       S - стоимость существующей в учреждении (части) системы обработки информации;

       S_спо - стоимость системы с учетом задач СПО.

Тогда стоимостные затраты на создание и эксплуатацию системы АСАСПИ будут определяться выражением:

                 S_спи=S_спо-S .                     (2.10)

С учетом выражения  (2.10) оптимизируемый функционал  имеет вид:

    S_спи=min k_iV_i+K_is_{i  .}                  (2.11)     

Математическая модель задачи выбора рациональной структуры и состава АСАСПИ формулируется следующим образом. Определить значение переменных c_{j l}, d_{j l}, e_{j l}, а также множества A_n и A_{n+1, j}, доставляющие минимум функционалу (2.11) при следующих ограничениях:

1) каждый пункт размещения ПЭВМ входит в одно и только в одно подмножество A_n

       A_n Ç А_m = 0, n ¹ m; n, m = 1, … , М;

2) загрузка каждого элемента системы должна быть меньше единицы

                   r_j<1, jÎA;

3) величины производительности процессоров V (пропускной способности каналов V_к) могут принимать только дискретные значения из допустимого множества {V}(V_к);

4) среднее время пребывания в системе задач пользователей n-го уровня не должно превышать предельно допустимого значения:

              U_n £ U_n^*, n=1, ... , М.

Величины r_j, U_n рассчитываются в соответствии с [25] для разомкнутой стохастической сети, в которой процессоры, внешние устройства и каналы связи представляются в виде модели систем массового обслуживания М/М/1. При этом принимаются традиционные допущения:

1)поток задач, поступающих на вход системы , простейший;

2)длительности решения задач в каждой из систем сети распределены по экспоненциальному закону;

3)длина очереди заявок на входе системы не ограничена.

Принятые допущения в настоящее время широко применяются при исследовании вычислительных систем, а их правомерность подтверждается результатами теоретических и экспериментальных исследований [25].

2.3. Обобщенный  алгоритм синтеза  системы сбора и анализа социально-психологической информации о состояниях воинских коллективов

Сложность решения  задачи синтеза АСАСПИ обусловлена тем, что в ней необходимо учитывать следующие факторы:

     1) стоимостные  затраты на создание и эксплуатацию системы;

     2) заданное  время U_n^* пребывания в системе задач пользователей n-го уровня.

     Указанные факторы  образуют  факторное пространство "стоимость-эффективность". Если решения задачи одновременно  удовлетворяют  всем  ограничениям  и относятся к числу эффективных,  то множество этих решений выбора рационального состава  и  структуры АСАСПИ принадлежат  области  Парето.  Так  как  решение Парето не единственное, то возникает задача выбора одного из них.

Ниже рассматривается один из возможных вариантов рационального выбора структуры и состава автоматизированной системы АСАСПИ,  в основу которого положены принципы векторной оптимизации.

Стоимость S(Х_G, Х_П) системы АСАСПИ будет определяться сочетанием рациональных значений  параметров  элементов системы и вариантов структуры системы. Тогда, принимая во внимание, что стоимость системы АСАСПИ и время U_n пребывания в системе задач  пользователей n-го уровня образуют векторный критерий качества АСАСПИ, в формализованном виде задача рационального выбора структуры и состава системы АСАСПИ может быть представлена в следующем виде:

                F(S,U_n)® opt;                   (2.12)

при условии 

                S(X_G⁰,Х_П⁰) £ S_доп ;                (2.13)

                U_n( X_G⁰,Х_П⁰) £ U_n^*;                (2.14)                                                          

где  S(X_G⁰,Х_П⁰) – стоимость системы, U_n(X_G⁰,Х_П⁰) - время пребывания в системе задач  пользователей n-го уровня.

Так как по своей природе указанные выше факторы противоречивы,  то решение задачи оптимизации функционала (2.12)  требует привлечения методов формализации компромиссов [10]. В рамках векторной оптимизации это противоречие разрешается путем свертки векторного функционала F(S,U_n) к скалярному критерию вида:

  F(S,U_n)=(1-S₀ (X_G⁰,Х_П⁰))´g₁+(1-U_n0(X_G⁰,Х_П⁰))´g₂,   (2.15)

           S₀=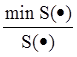;   U_n0=;

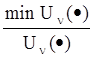где S₀(·), U_n0(·) - нормированные значения стоимостных затрат на создание и эксплуатацию системы и  времени  пребывания  задач  в системе;

min S(X_G⁰,Х_П⁰)  - минимальный уровень стоимостных затрат, при которых время   пребывания   задач   в   системе  равно U_n*;

min U_n (X_G⁰,Х_П⁰) - минимальное время пребывания задач в системе при  условии максимальной автоматизации решения задач СПО;

 g_1, g₂ – коэффициенты ранжировки критериев.

     Величины min U_n (X_G⁰,Х_П⁰ ) и min S(X_G⁰,Х_П⁰)  образуют идеальный вектор эффективности системы АСАСПИ.  Составляющие идеального  вектора  эффективности  интерпретируются как результаты решения прямой и обратной задач вида:

     а)S(X_G⁰,Х_П⁰) ® min;                        (2.16)                                               

при условиях    U_n (X_G⁰,Х_П⁰) £ U_n^*;

                S(X_G⁰,Х_П⁰) £ S_доп;