Случайные события (Понятие случайного события. Вероятность случайного события. Основные теоремы и формулы. Повторение испытаний)

Глава 1. СЛУЧАЙНЫЕ СОБЫТИЯ

1.1. Понятие случайного события

1.1.1. Определение случайного события

До сих пор мы имели дело с явлениями или событиями, которые происходили всякий раз при реализации некоторого комплекса условий S.

Например, если воду при нормальном атмосферном давлении p = 760 мм ртутного столба разогреть до температуры 100 °С (комплекс условий S), то она превратится в пар (событие А).

Или, если в некоторой δ - окрестности точки (x₀, y₀) существуют непрерывные частные производные функции z = f(x, y) (комплекс условий S), то эта функция дифференцируема в точке (x₀, y₀) (событие А).

Если в результате эксперимента всякий раз происходит некоторое событие, то это событие называется достоверным(обозначается ).

Если в результате эксперимента некоторое событие не происходит никогда, то оно называется невозможным (обозначается ).

Если в результате эксперимента событие может произойти, либо не произойти, то оно называется случайным (обозначается А, В, С, …).

Теория вероятностей изучает случайные события, которые можно наблюдать неограниченное число раз при одних и тех же условиях, и не рассматривает случайных уникальных событий.

1.1.2. Пространство элементарных исходов

Выше мы выяснили, что с каждым случайным событием связан некоторый опыт или эксперимент.

Множество всевозможных, взаимоисключающих исходов (результатов) эксперимента называется пространством элементарных исходов или элементарных событий (обозначается ).

Пример 1.1. Эксперимент – подбрасывание монеты.

Возможны два исхода:  – монета выпала гербом,  – монета выпала надписью, пространство элементарных исходов – .

Пример 1.2. Эксперимент – подбрасывание игральной кости.

Элементарные исходы:  – на выпавшей грани игральной кости – i очков, , пространство элементарных исходов – .

Пример 1.3. Эксперимент – извлечение карты из тщательно перемешанной колоды.

Элементарные исходы:  – карта определенной масти и определенного достоинства , пространство элементарных исходов – .

Пример 1.4. Эксперимент – регистрация вызовов в течение часа на АТС.

Элементарные исходы:  – в течение часа на АТС поступило i вызовов, пространство элементарных исходов – .

Пример 1.5. Эксперимент – стрельба по плоской мишени.

Элементарные исходы:  – точки некоторой области на плоскости, пространство элементарных исходов – .

В первых трех примерах пространство элементарных исходов - конечное, в четвертом – бесконечное, но счетное, в пятом – бесконечное и несчетное.

1.1.3. Алгебра случайных событий

Назовем некоторый элементарный исход эксперимента благоприятствующим событию А, если в результате эксперимента, в котором имел место данный элементарный исход, происходит событие А.

Тогда любое случайное событие можно представить как совокупность (множество) случайных исходов, благоприятствующих этому событию, т.е. как некоторое подмножество из пространства элементарных событий .

Например, в примере 1.2 можно рассмотреть событие А – на грани игральной кости выпало число очков кратное 3, тогда это событие представляется как совокупность двух элементарных исходов .

В примере 1.3 – событие А – из колоды карт извлечен туз (каждая девятая карта в масти), тогда .

В примере 1.4 – событие А – в течение часа поступило не более 10 вызовов, тогда .

В примере 1.5  –  событие А  – произошло попадание в круг радиуса R = 1, здесь .

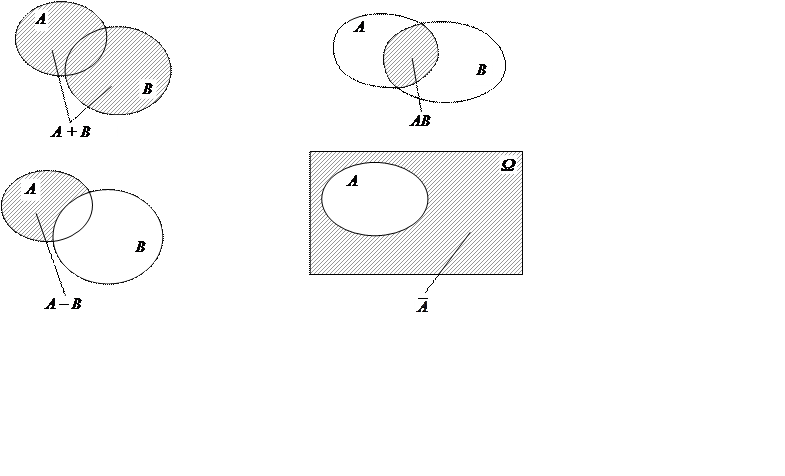
Суммой А + В (АВ) случайных событий А и В называется случайное событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий, т.е. в результате эксперимента происходит хотя бы одно событие.

Произведением А•В (АВ) случайных событий А и В называется случайное событие, состоящее из элементарных исходов, благоприятствующих и событию А, и событию В, т.е. в результате эксперимента события А и В происходят одновременно.

Разностью А – В (А\В) случайных событий А и В называется случайное событие, состоящее из элементарных исходов, которые благоприятствуют событию А и не благоприятствуют событию В, т.е. в результате эксперимента происходит событие А и не происходит событие В.

События А и В называются несовместными, если нет элементарных исходов, благоприятствующих и событию А, и событию В, т.е. в результате эксперимента эти события не могут произойти одновременно или .

Событие  называется противоположным событию А, если выполняются два условия:  1)  ,  2)  .

Если каждому элементарному исходу поставить в соответствие некоторую точку на плоскости, то пространство элементарных исходов и любое случайное событие изобразятся некоторыми множествами точек на плоскости, что дает наглядное представление о введенных арифметических операциях. Эти рисунки называются диаграммами Вьена.

Основные свойства введенных операций

1. Коммутативный закон (перестановочное свойство):

,  .

2. Ассоциативный закон (сочетательное свойство)

,  .

3. Дистрибутивный закон (распределительное свойство)

.

4. Правила де Моргана

,  .

5. , , , , , .

Все свойства доказываются непосредственно из определений операций, необходимо рассмотреть произвольный элементарный исход, благоприятствующий левой части равенства, и показать, что он благоприятствует и правой части тоже, и наоборот. Кроме того, при доказательстве можно использовать диаграммы Вьена. Для этого необходимо изобразить множества элементарных исходов, благоприятствующих левой и правой части на разных картинках, и визуально убедиться, что они совпадают. Покажем, например, что справедливо равенство .

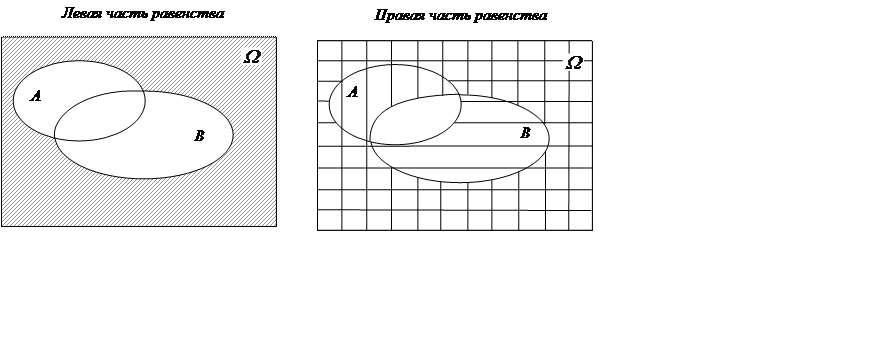Фигуры, заштрихованные на диаграммах, совпадают, значит  .

Система (совокупность) случайных событий Â называется алгеброй случайных событий, если   выполняются свойства:

,

,

,

.

Таким образом, алгебра случайных событий - это множество случайных событий, содержащее достоверное событие и замкнутое относительно операций сложения и умножения.

Наиболее простой алгеброй случайных событий является множество, состоящее из двух событий: .

В дальнейшем везде будет использоваться алгебра случайных событий, которая является множеством всевозможных подмножеств из пространства элементарных событий  (легко проверить, что все свойства в определении алгебры случайных событий выполняются для этого множества).

Утверждение 1.1. В алгебре с конечным числом элементов в пространстве элементарных исходов  случайных событий.

Доказательство. Каждому случайному событию можно однозначно сопоставить последовательность из 0 и 1 длины n по следующему правилу.

Если i-й элементарный исход благоприятствует событию А (ω_i Î А), то на i-м месте в последовательности ставится 1, если не благоприятствует событию А (ω_i Ï А), то на i-м месте ставится 0.

Таким образом, перебираются все последовательности из 0 и 1 длины n, а таких последовательностей будет  штук.

1.2. Вероятность случайного события

Числовая характеристика возможности появления случайного события в эксперименте называется вероятностью этого события.

1.2.1. Аксиоматическое определение и простейшие следствия из аксиом