Виды машинных циклов. Слово состояния процессора. Слово состояния МП КР580ВМ80А. Ввод-вывод в режиме прерывания. Алгоритм обслуживания прерываний, страница 27

Строго говоря, понятие «бит» введено для измерения количества информации, получаемой при осуществлении одного из двух равновероятных событий. Но использование этого понятия для обозначения двоичного разряда допускается.

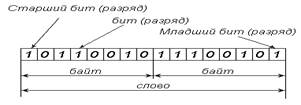
Байт. Развитие вычислительной и информационной техники вызвало появление 8-битовой единицы для обмена информацией между устройствами. Такая 8-битовая единица носит название байт. Многие типы цифровых вычислительных устройств и систем обработки информации используют числа из 8, 16, 24 или 32 и более бит (1, 2, 3 или 4 и более байта). Таким образом, двоичное число, показанное на рис. 2.1, состоит из 2 байт.

Половина байта (4 разряда) получила название «тетрада».

Слово. Вычислительная машина содержит большое количество ячеек, регистров и других устройств для хранения и обработки информации. Большинство устройств имеют одинаковую разрядную «длину» n. Каждое устройство используется для обработки или хранения одновременно n бит двоичной информации. Информация, хранимая или обрабатываемая в одном таком устройстве, называется словом. Пример слова 16-битовой вычислительной машины приведено на рис. 2.1.

Нахождение десятичного эквивалента двоичного числа уже было рассмотрено. Задача обратного перевода решается несколько сложнее, причем разными методами. Наиболее понятный (но не самый простой) метод предполагает последовательное определение максимальной степени числа два исходного десятичного числа и получающихся после этого остатков. Получающиеся степени двойки определяют местоположение единиц в двоичном числе. В остальных разрядах этого двоичного числа записываются нули. Для примера рассмотрим перевод в двоичную форму таким способом числа 53.

Максимальная степень числа два в исходном числе – 5:

2⁵ = 32.

После вычитания тридцати двух из исходного числа получаем остаток – 21. Максимальная степень числа два в этом числе – 4:

2⁴ = 16.

Далее поступаем аналогично: максимальная степень числа два в остатке (число пять) – 2:

2² = 4, а в последнем остатке, равном единице – 0:

2⁰ = 1.

Таким образом, число 53 можно представить как сумму полученных выше чисел:

53 = 32 + 16 + 4 + 1 = 2⁵ + 2⁴ + 2² + 2⁰.

Используя все степени числа два от нулевой до пятой, исходное число можно представить следующей суммой:

53 = 1´2⁵ + 1´2⁴ + 0´2³ + 1´2² + 0´2¹ + 1´2⁰.

Так как двойка является основанием той системы счисления, в которую мы переводим число 53, полученные единицы и нули в соответствующих разрядах дадут искомое двоичное число:

53D = 110101В.

Проще этот же результат можно получить, воспользовавшись методом деления, который предполагает последовательное деление числа на 2 и учет получающихся при этом остатков. Деление производят до тех пор, пока результат не уменьшится до единицы. Полученная последовательность остатков из нулей и единиц, включая последнюю единицу, записанная «наоборот», является двоичным эквивалентом десятичного числа.

Для примера рассмотрим перевод в двоичную форму методом деления того же числа 53:

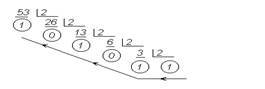
Прочитав результат, начиная с последней единицы, получим

53D = 110101B.

2.3. Восьмеричная система счисления.

В восьмеричной системе счисления основание системы равно восьми, что определяет общее количество цифр в этой системе – от 0 до 7. Соответственно, веса разрядов представляют собой степени числа 8: 8⁰ = 1, 8¹ = 8, 8² = 64, 8³ = 512, и т. д.

Для обозначения чисел в восьмеричной системе используется либо подстрочный символ 8, либо буква Q: 165₈ = 165Q.

Перевод чисел из восьмеричной системы в десятичную и обратно производится по правилам, подобным уже описанным ранее. Связь же между восьмеричной и двоичной системами позволяет переходить от одной системы к другой очень просто. Основана эта связь на том, что число 8 является целой степенью числа 2.

Для перевода числа из восьмеричной системы в двоичную достаточно все цифры восьмеричного числа представить трехразрядным двоичным числом и записать их в том же порядке. Три разряда используются и в тех случаях, когда приходится писать незначащие нули слева, за исключением самого старшего разряда восьмеричного числа.