Типовые звенья в устройствах цифровой обработки сигналов. Структурные схемы рекурсивного цифрового фильтра в прямой форме

ТИПОВЫЕ ЗВЕНЬЯ В УСТРОЙСТВАХ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

Устройства цифровой обработки сигналов в радиоприемниках обычно состоят из типовых звеньев (элементов), которые, будучи соединенными по определенным схемам, образуют различные алгоритмы цифровой обработки сигналов. К таким звеньям относятся фильтры, преобразователи Гильберта, амплитудные ограничители, цифровые генераторы и т.д. Рассмотрим реализацию этих звеньев в цифровых вычислительных устройствах (ЦВУ).

7.3.1. ЦИФРОВЫЕ ФИЛЬТРЫ

Цифровые фильтры из-за ограниченной разрядности используемых чисел и возникающих в них шумов квантования, строго говоря, не являются линейными. Однако при определенных уcло

виях указанные эффекты можно существенно ослабить, поэтому описываемые ниже цифровые фильтры будем считать линейными.

Нерекурсивными называются фильтры без обратных связей (см. § 3.12), работа которых задается разностным уравнением

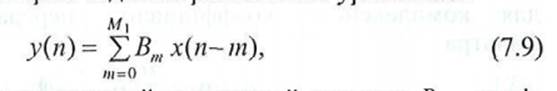
где х(п),у(п) — цифровые входной и выходной сигналы; В_т — коэффициенты; п — номер отсчета; т — задержка; М\— порядок фильтра.

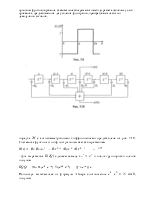
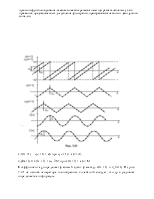
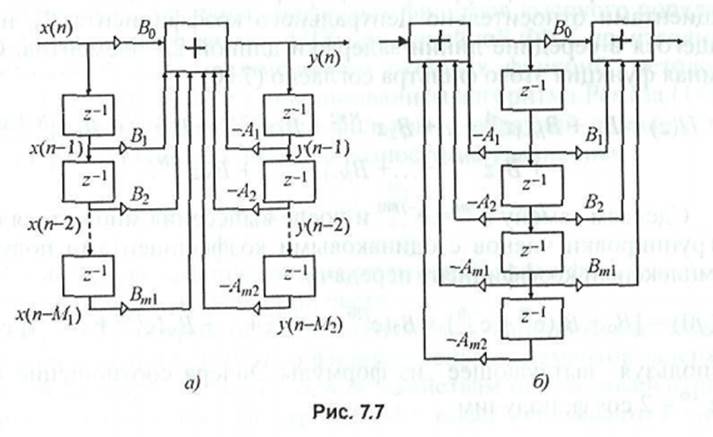
Структурные схемы рекурсивного цифрового фильтра в прямой форме {а) и в канонической форме (б) представлены на рис. 7.7. Схема нерекурсивного фильтра получается как частный случай из схемы на рис. 7.7, а, если в ней все коэффициенты А_т равны нулю, т.е. нет обратных связей.

Для описания свойств нерекурсивных фильтров широко используется аппарат Z-преобразований, позволяющий от разностных уравнений перейти к алгебраическим [3]. Для этого вводится понятие функции передачи цифровых фильтров, которая получила название системной функции H(z). Она равна отношению Z-преобразований Y(z) и X(z) от сигналов у(п) и х(п) и связана с коэффициентами фильтра следующим соотношением

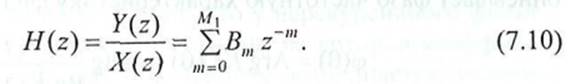
Связь между (7.9) и (7.10) легко устанавливается из двух свойств Z-преобразования — линейности и смещения во времени. Из H(z) можно получить выражение для комплексного коэффициента передачи фильтра K(jQ) при гармоническом воздействии на его входе в установившемся режиме. Для этого в (7.10) сделаем замену

где 0 = <S)T_a ~ нормированная к частоте дискретизации частота входного сигнала. Подставим (7.11) в (7.10) и получим выражение для комплексного коэффициента передачи нерекурсивного фильтра

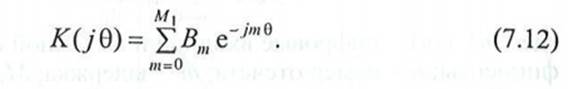
Применяя формулу е^_/'"⁰⁼ cos mQ - j sin mQ, представим K(JQ) как сумму действительной и мнимой частей:

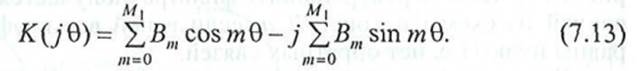
Модуль K(jQ) описывает амплитудно-частотную характеристику фильтра

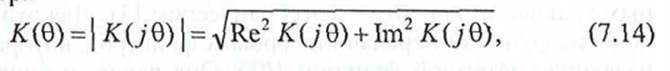
где Re K(jQ) = £в_и1 cos ?n9, Im KQ'O) = §B,₍₁ sin mB, а аргумент /C(j6)

w = 0 шцО

описывает фазо частотную характеристику фильтра

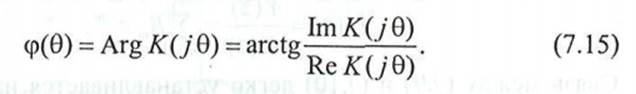
Наибольший практический интерес представляют нерекурсивные фильтры с линейной фазочастотной характеристикой. Коэффициенты таких фильтров должны быть симметричны или антисимметричны относительно середины линии задержки фильтра.

Рассмотрим нерекурсивные фильтры с симметричными коэффициентами относительно центрального коэффициента В₀, находящегося в середине линии задержки длиной 2N элементов. Системная функция этого фильтра согласно (7.10)

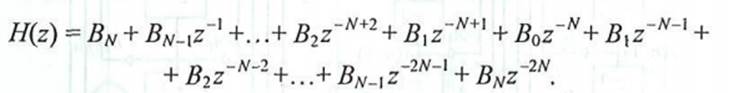
Сделаем замену z~"' - e~""° и после вынесения множителя e"^/We и группировки членов с одинаковыми коэффициентами получим комплексный коэффициент передачи

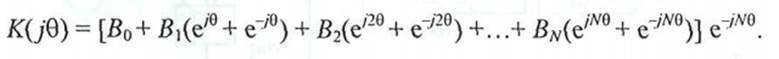
Используя вытекающее из формулы Эйлера соотношение е^/ч> + + е~-^/ф= 2 cos ф, получим

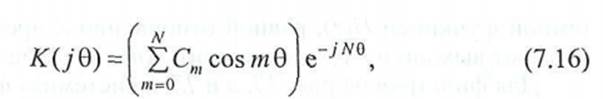
Согласно (7.14) АЧХ фильтра описывается формулой

Из выражения для K(Q) следует, что у нерекурсивного фильтра второго порядка существует частота 9,„ на которой коэффициент передачи ЛГ(6„) = 0. На этой частоте выполняется условие Bq+ 2 cos 0„= 0. Отсюда получим формулу для расчета центрального коэффициента фильтра В₀, который определяет частоту 8„ нулевого коэффициента передачи K(Q):

В₀ =- 2 cos 9„.

Синтез нерекурсивных цифровых фильтров высокого порядка по заданным требованиям к АЧХ при линейной ФЧХ производится методом Фурье с применением оконных функций, методом наименьших квадратов и с использованием алгоритма Ремеза [14].

Рекурсивными называются фильтры с обратной связью (см. рис. 7.7), работа которых задается разностным уравнением

У (") = S В_т х (п - т) -1 А_т у (и - т).

Здесь В_т ~ коэффициенты нерекурсивной части фильтра; А_т -коэффициенты его рекурсивной части.

На рис. 7.7, б приведена так называемая каноническая схема рекурсивного фильтра. В этом фильтре меньше элементов задержки, чем в фильтре на рис. 7.7, а, а по свойствам они эквивалентны. Рекурсивные цифровые фильтры (РЦФ) также описываются системной функцией H(z), равной отношению Z-преобразований Y(z) и X{z) от выходного у(п) и входного х(п) сигналов фильтра. Для фильтров на рис. 7.7, а и 7.7, б системная функция