Типовые звенья в устройствах цифровой обработки сигналов. Структурные схемы рекурсивного цифрового фильтра в прямой форме, страница 2

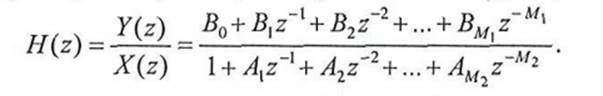
Из разных методов расчета цифровых фильтров наибольшее распространение получил метод расчета РЦФ по аналоговому прототипу с применением билинейного преобразования. Вместе с тем в устройствах цифровой обработки сигналов довольно часто применяются двухконтурные и даже одноконтурные РЦФ. Такие фильтры могут быть рассчитаны по методу прямого синтеза. Проиллюстрируем это на примере.

Необходимо определить коэффициенты А\,А₂ РЦФ второго порядка по известным резонансной частоте 9о и нижней границе полосы пропускания 0] при заданной неравномерности а в полосе пропускания.

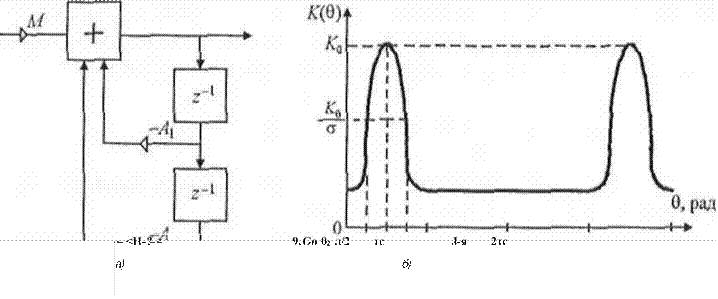
Структурная схема рекурсивного цифрового фильтра второго порядка {а) и его амплитудно-частотная характеристика (б) представлены на рис. 7.8. Системная функция РЦФ второго порядка (рис. 7.8, а)

где z_x = Re~'°⁰, z\ = Re'⁰ - комплексно-сопряженные полюса системной функции РЦФ в полярных координатах; R - расстояние от начала координат до полюса в z - плоскости; Qq-ItiFoIF^ - нормированная к частоте дискретизации безразмерная частота резонанса. Из (7.19) следуют формулы, связывающие параметры R и 9₀ с коэффициентами РЦФА\ иА₂:

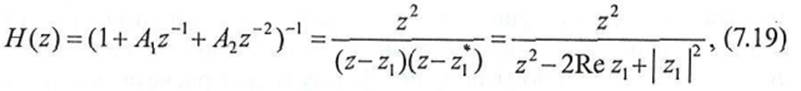
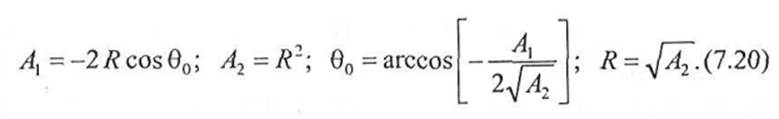
Для перехода от H(z) к комплексному коэффициенту передачи Ду'0) необходимо в (7.19) сделать замену z = e^/0, где 0 = соАР_д -нормированная к F_a безразмерная частота. В результате этой замены получим:

Дув) = [(1 -Re^^Xl -Re-^y(9+Qo)r\

■

Амплитудно-частотная характеристика РЦФ второго порядка есть модуль от Ду'О) и описывается выражением

Д0) = {[1 +R²~2Rcos (0-0_о)][1 + R²~2R cos (0 + 0_О)]}"^1/2.(7.21)

Построенная по этому выражению АЧХ для РЦФ второго порядка приведена на рис. 7.8, б. Зададимся неравномерностью а на нижней границе Oi полосы пропускания РЦФ и получим уравнение

-^- = а,         (7.22)

Щ)

где К₀= [(1 -R)²(l + R²-2R cos 20_о)]~^,/2 - коэффициент передачи РЦФ на резонансной частоте 0_О.

Возведем левую и правую части (7.22) в квадрат и с учетом (7.21) получим уравнение о²(1 - R)\l +R²-2R cos 20_о) =

= [I + R²-2R cos (0, - 0„)][i + R²- 2R cos (0, - 0_O)].

После преобразований и замены переменной а²х(х + А) = (х + £,)(* + С,), (7.23)

гдех = ^{]~^R)2 ■ 4=1-cos 20_о; Я, -1- cos (0,- 0_О); С, =1- cos (0, + 8₀). 2 R

Av²~B>~C

Решим (7.23) относительно х. В результате

x = (p² + q)^V2-p, где р =

2(о²-1)        сг-1

Тогда^=1-+-х-[(1+х)²-1]^1/2.

Зная R и 0о, по (7.20) определим коэффициенты А\ и А₂ РЦФ. Для обеспечения на частоте 0о единичного коэффициента передачи множитель М на входе РЦФ рассчитывается по формуле М=\/Ко.

7.3.2. ПРЕОБРАЗОВАТЕЛЬ ГИЛЬБЕРТА

Преобразователь Гильберта (ПГ) создает фазовый сдвиг между составляющими спектра выходных сигналов, равный тс/2. Таким образом ПГ можно использовать для получения комплексного сигнала

v(n) = x(n)-jx(n),       (7.24)

где jx{n) - сопряженный по Гильберту цифровой сигнал от сигнала х(п).

Сигналы х(п) и jx(n) называют парой квадратурных компонент цифрового сигнала, так как умножение на мнимую единицу j эквивалентно фазовому сдвигу всех спектральных компонент сигнала х(п) на я/2.

Из (7.24) следует, что идеальный ПГ должен иметь комплексный коэффициент передачи

I   у,   7t < 0 < 271.

На рис. 7.9 представлена зависимость комплексного коэффициента передачи идеального ПГ. Рассмотрим построение ПГ на нерекурсивном фильтре порядка 2N с антисимметричными коэффициентами В_т. Структурная схема ПГ на нерекурсивном фильтре

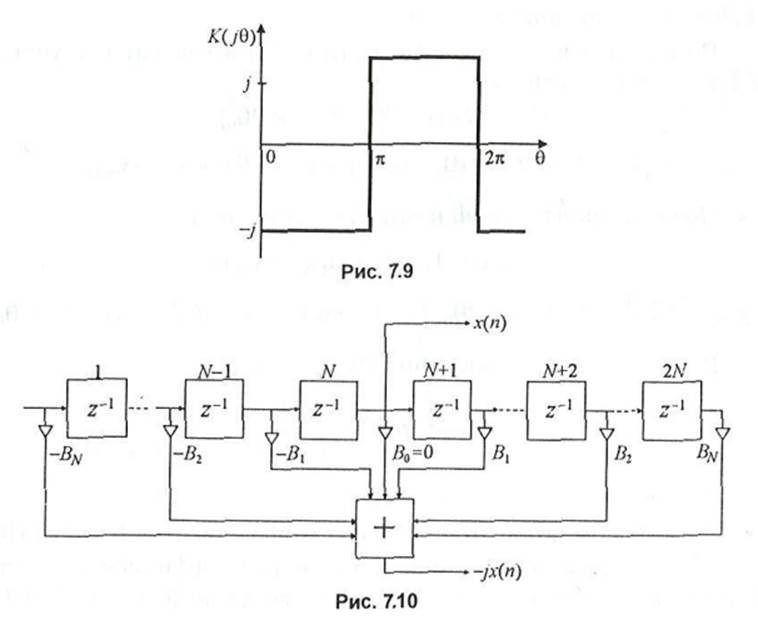
порядка 2N с антисимметричными коэффициентами представлена на рис. 7.10. Системная функция этого фильтра описывается выражением

H(z) = -B_N-B_N._lz~¹ -...-B_lZ-^N+l +B_Qz-^N +B_lZ'^N- ¹        »    ^2Л