откуда получим формулу, связывающую an с частотой Fr=\/Tr пилообразного колебания
Как видно из рис. 7.18 и формулы (7.28), основу генератора пилы составляет накапливающий сумматор по модулю М. При реализации этого генератора программно по (7.28) следует задавать модуль суммирования М, например М= 0,5 или М= 1. Однако в реальных вычислителях из-за ограниченного числа разрядов возникает переполнение разрядной сетки, поэтому в них условный переход в программе можно опустить. В этом случае число М определяется наибольшим операндом, представляемым в вычислителе с фиксированной запятой, и сброс от +Мдо -М будет происходить автоматически при переполнении в аккумуляторе вычислителя.
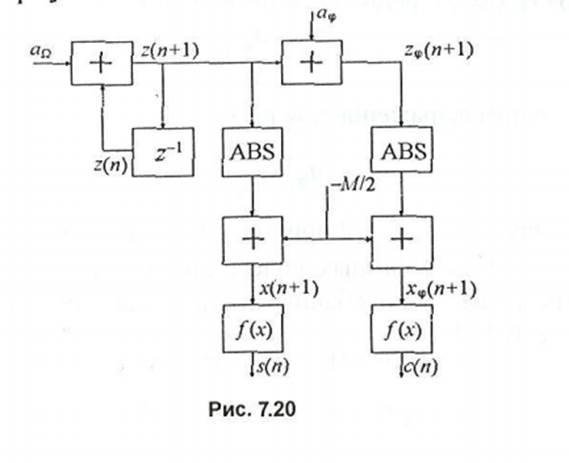
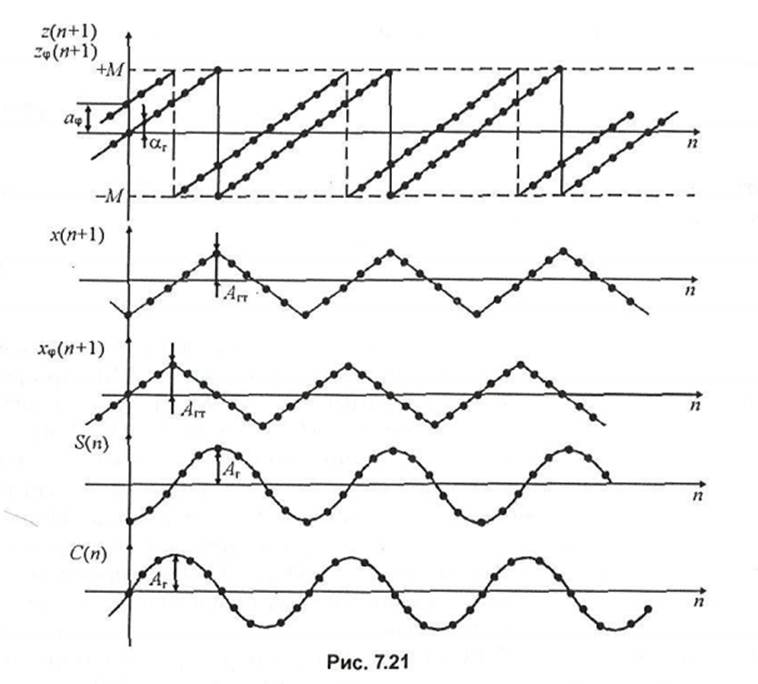
Теперь рассмотрим управляемый по частоте косинусно-синусный генератор (УКСГ) на основе генератора пилообразных колебаний. Структурная схема такого генератора приведена на рис. 7.20, а на рис. 7.21 - временные диаграммы, поясняющие его работу.
Исходное пилообразное колебание z(n+\) формируется по разностным уравнениям (7.28). Из него получаем другое пилообразное колебание z,p(« +1) с фазовым сдвигом ф относительно исходного по формулам
z(P(n +1) = z(« +1) + аф при z(« +1) + яф < Л/,
z,p(n +1) = z{n + \) + av- 2М при z(n +1) + аф > М.
Коэффициент яф определяет фазовый сдвиг ф между z(n +1) и z(p(/z+l). Из рис. 7.21 на основе генератора пилообразных колебаний следует, что (р в радианах определяется по формуле фнА*, (7.31) М
откуда получим выражение для расчета коэффициента а9
«,=^. (7.32)
Я
Для получения ф = я/2 при М - 1 коэффициент яф = 1/2.
Далее из пилообразных колебаний z(n + \) и z<p(// + l) формируются треугольные колебания х и хф без постоянной составляющей по формулам:
х(л+1) = |2(л+1)|-М/2,
*ф(и +1) = | гф(л +1) \-М/2.
(7.33)
Затем с помощью нелинейного функционального преобразования fix) из колебаний х и х(р формируются квадратурные квазигармонические колебания с(п) и s(n).
Одним из вариантов преобразования Да-) является применение полиномов Чебышева первого рода Тт{х) нечетных степеней т, так как графики этих полиномов симметричны относительно начала координат.
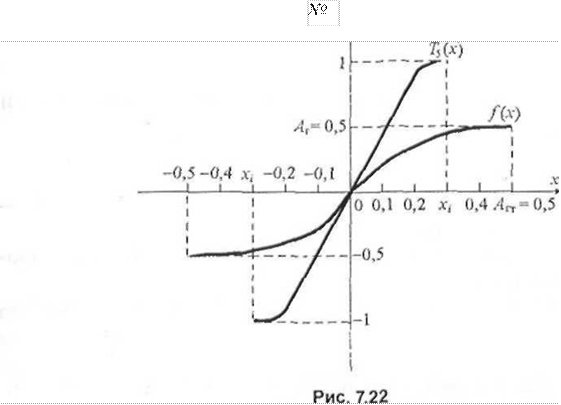
Приведем алгоритм получения выражения f(x) с применением полиномов Чебышева Тт(х). Графики полинома Чебышева пятой степени Т5(х) и измененной в масштабах по осям абсцисс и ординат функцииДд;) при А1.=АП = 0,5 приведены на рис. 7.22.
1. Выберем степень полинома m по требуемому ослаблению амплитуд высших гармоник Ak в спектре формируемых колебаний относительно амплитуды первой гармоники А,- из соотношения [3]
у к=А=к'ы+]\ А
где /с=3,5,7... - номера высших гармоник. Обычно принимают&=3 для наиболее интенсивной по амплитуде третьей гармоники. Тогда
Ink
2. Определим абсциссу ближайшего справа от начала координат экстремума полинома Т1П(х) по формуле я-, = cos (ln/m), где / = (m -1)/2.
3. Изменим масштаб полинома Т„,(х) по оси ординат для получения нужной амплитуды колебаний Аг по соотношению
Ux) = ArTm{x).
4. Изменим масштаб полинома по оси хъ q раз, где q =х]/Агт и получим искомое выражение
f{x)=±Arrm(qx), где знак "+" для m = 5, 9, 13..., а знак "-" для m = 3, 7, 11...; 4гт -амплитуда треугольных колебаний (см. рис. 7.21).
5. Приведем Дх) к гнездовой форме для уменьшения программных затрат при вычислении Дх).
Пример. Дано Аг~Ап= 0,5; у3= 1/700. Надо найти выражение Дх).
Решение.
Степень полинома m > (In 700/ln 3) -1 > 4,96, примем m = 5.
/ = (m -1)72, x, = cos (ln/m) = 0,309017.
З.Д(х) =ЛГВД = 0,5(16x5- 20x3 + 5x) = 8x5- 10x3 = 2,5*.
4=*,/^ = 0,618034, Дх) = 8(r/x)5-l 0(qxf + 2,5qx = 0,72136x5--2,36068x3 + l,545085x.
2x(0,7725425 - (2x)2(0,295085 - 0,0225425(2x)2)).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.