У о =
а а
1 + (3|б| |я|>|А| а|б|+р|а| | й | < | b |,
где а = 0,96046, р = 0,39783.
Пример. А = 0,85 = 0,6 + 0,25. Тогда у0 = 0,6757335; .у, = 0,8724256; ^ = 0,916862;
^з = 0,921514; у4 = 0,921922; у5 = 0,921952;
у6 = 0,9219542; у-, = 0,92195443.
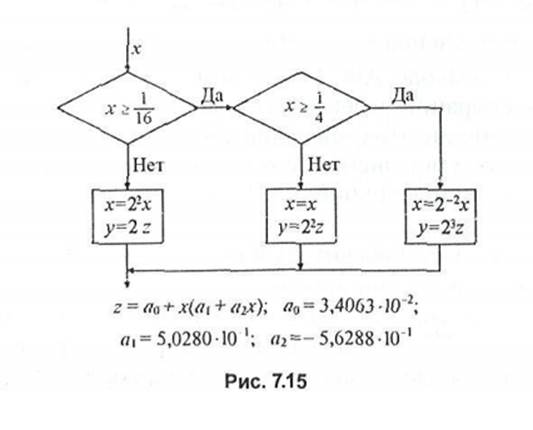
Точное значение -^0,85 = 0,92195444. Как видно из этого примера, практически точный результат получился лишь на седьмом шаге итерации. Более экономного по программным затратам вычисления корня квадратного можно достичь, если представить отрезок функции у = yfx в виде степенного полинома
. ч .
у ~ а() + ахх + а2х +а3х +...= ^акх . (7.25)
Коэффициенты полинома можно найти различными методами (методом наименьших квадратов, разложением по биному Ньютона, методом экономизации по Чебышеву и т.д.).
Представим функцию у - -fx полиномом второго порядка в удобном для вычислений на процессоре виде у - а0 + ci\X + х(\ -х).
Если задать диапазон изменения числа х в интервале 0,1 <х < 0.4, то полученные методом наименьших квадратов коэффициенты
«0 = 0,1736; а, =0,5491.
Расчеты показывают, что наибольшая относительная погрешность вычисления функции у = 4х по этой формуле в интервале изменения х от 0,1 до 0,4 не превышает 1,33 %. С расширением
интервала изменения х погрешность возрастает. Для ее уменьшения можно увеличивать степень полинома или применить процедуру вычислений с условными переходами. Идея ее состоит в следующем. Сравнительно небольшой по изменению аргумента х(х\<х<х2) отрезок функции у = 4х представляется степенным полиномом с найденными каким-либо способом коэффициентами ак. Затем входное число х сравнивается с числами xt и х2, причем хг1х\ < 2и, где « = 1,2, и определяется положение числа х на числовой оси относительно этих чисел. Далее число х умножается на такое известное число 2*", чтобы выполнилось условие хх<2±их<Х2, (7.26)
где Х),х2 - границы изменения аргумента функции у = -fx, представленной полиномом (7.25). После этого вычисляется значение .у при аргументе 2±пх и результат умножается на число 2г"/2, так как у = v2~" х • 2+"12 = V*.
Поясним это примером. Пусть a'i = 0,25; лг2 = 0,5, а входное число х = 0,01. Чтобы произведение 2~"х попало в интервал 0,25...0,50, умножим число.* = 0,01 на 2s и получим новое значение аргумента х = 0,01-2 = 0,32. Затем при х = 0,32 вычислим у = 0,5669 и, умножив его на число 2_5/2 = —]-=*= 0,1767767, получим
4V2
результат 0,1002. Точное значение л/0,01 = 0,1 лишь на 0,2 % отличается от полученного результата.
На рис. 7.15 приведена структурная схема одного из возможных алгоритмов приближенного вычисления квадратного корня у = л/х при изменении х от 0 до 1.
7.3.5 ЦИФРОВЫЕ АМПЛИТУДНЫЕ ОГРАНИЧИТЕЛИ
Назначение цифровых амплитудных ограничителей (АО) состоит в обеспечении стабильности амплитуды цифрового сигнала на их выходе при изменяющейся амплитуде цифрового сигнала на входе АО. На рис. 7.16 приведена укрупненная структурная схема цифрового АО. В ее состав входят преобразователь Гильберта (ПГ) на входе, блок вычисления квадрата амплитуды А', блок вычисления чисел -т==г=— и два перемножителя.
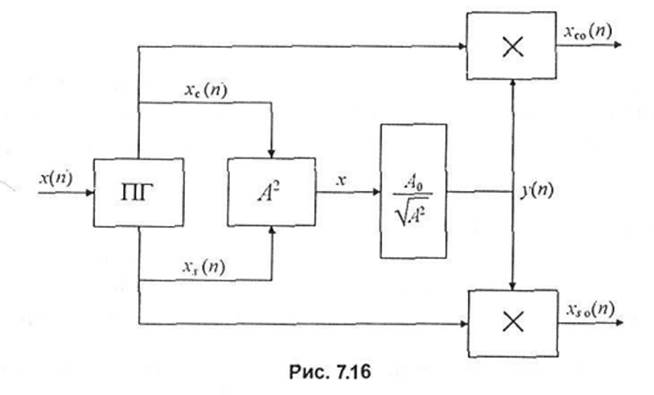 Если
на вход АО поступают
выборки из сигнала х(п), то на
выходах ПГ получим квадратурные компоненты из сигнала хс(п)
= =А(п) cos nQ и xs(n) ~A{ri) sin nQ.
Если
на вход АО поступают
выборки из сигнала х(п), то на
выходах ПГ получим квадратурные компоненты из сигнала хс(п)
= =А(п) cos nQ и xs(n) ~A{ri) sin nQ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.