Решение дифференциальных уравнений. Множество решений дифференциального уравнения. Решение дифференциальных уравнений методом Эйлера

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1 Решение дифференциальных уравнений

  1.1.1 Постановка задачи.

Уравнения, содержащие неизвестную функцию и её производные, называются дифференциальными. Простейшим дифференциальным уравнением является уравнение первого порядка:

y’=f(x,y)                                                                                                   (1.1)

Основная задача, связанная с этим уравнением, известна как задача Коши: найти решение уравнения (1.1) в виде функции y(x), удовлетворяющей начальному условию:

y(x₀)=y₀                                                                                                     (1.2)

Функция y(x₀)= f(x) называется решением дифференциального уравнения, если при подстановке её в уравнение (1.1) она превращает его в тождество. Для нахождения единственного решения задают начальные условия – значения функции y(x)=y₀ в некоторой точке x₀ . На рисунке 1.1 дана геометрическая интерпретация множественности решения дифференциального уравнения первого порядка типа (1.1). Задание начального значения позволяет из множества решений выбирать одно.

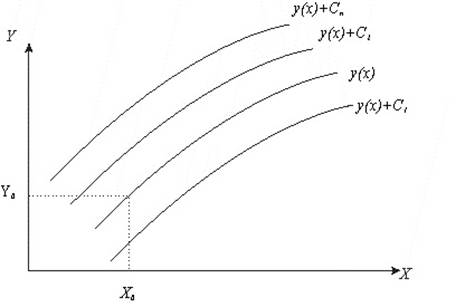
Рисунок 1.1 – Множество решений дифференциального уравнения.

Численные методы решения дифференциальных уравнений дают возможность искать решение в виде таблицы значений функции y(x) для независимой переменной х из промежутка х₀<x_i<x₀+a. Значение узлов интегрирования дифференциального уравнения определяется как

x_i+1 = x_i + Dx

,где Dx – приращение независимого аргумента, устанавливается заранее, либо выбирается последовательно в процессе нахождения приближенного решения.

Тогда значение искомой функции y(x) в узлах x_i+1 определяют как

y(x_i+1) + Dy_i;               y(x₀) = y₀

,где Dy_i – приращение функции y(x), вызванное приращением независимого аргумента Dx_i.

Все численные методы отличаются в основном друг от друга подходом к вычислению приращения Dy_i.

1.1.2. Решение дифференциальных уравнений методом Эйлера.

Это простейший метод решения  дифференциального уравнения первого порядка в постановке Коши. Метод основан на разложении y(x)  в ряд Тейлора в окрестностях точки x₀:

y(x₀+h) = y(x₀) + hy’(x₀) + ½ h²y’’(x₀) +…

Если h=Dx достаточно мало, то членами, содержащими во второй и более высоких степенях можно пренебречь. Тогда

y(x₀+h) = y(x₀) + hy’(x₀)        или

y₁ = y_n + hf(x₀, y₀)

Продолжим этот процесс, используя соотношения:

y_n+1=y_n+h f(x_n,y_n),        n=1,2,…

Итак, приращение функции y(x) при изменении независимого аргумента на h в методе Эйлера равно

Dy_i=hf(x_i,y_i)

С геометрической точки зрения это означает, что точное решение дифференциального уравнения, представляющего собой интегральную кривую y=j(x), на каждом интервале заменяется отрезком прямой – касательной к точкам x₀, y₀, x₁, y₁,…, x_n, y_n.

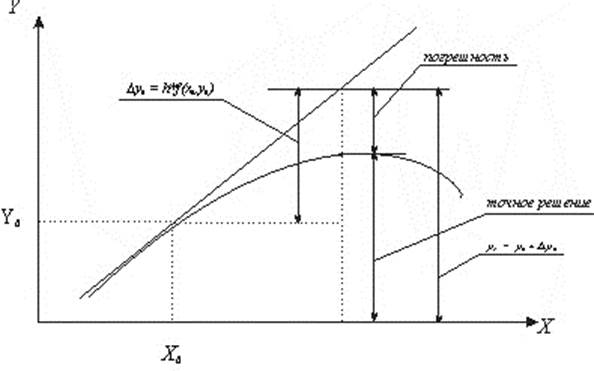
Рисунок 1.2 - Графическая интерпретация метода Эйлера.

Таким образом, график численного решения  представляет собой последовательность коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y=j(x).

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага систематически возрастает. Локальная погрешность этого метода (погрешность на одном шаге) пропорциональна h², глобальная погрешность (погрешность на всём интервале) пропорциональна h – первому порядку точности.

1.2. Аппроксимация. Метод наименьших квадратов

1.2.1.Постановка задачи.

Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости

Таблица 1.1

Нужно найти формулу, выражающую эту зависимость аналитически. Можно применить метод интерполяции. Однако совпадение значений интерполяционного полинома и исходной функции в узлах интерполяции x₁, x₂,…,x_n  не всегда означает совпадение характеров поведения исходной и интерполирующей функции. Так уже при степени полинома выше 5 –6 он не редко ведёт себя непредсказуемо в промежутках между узлами. В результате получается характерная волнистость, не свойственная самой функции.

Поставим задачу так, чтобы с самого начала обязательно учитывался характер исходной функции: найти функцию заданного вида

y=F(x)                                                                                                                   (1.3)

, которая в точке x₁x₂,…, x_n принимает значение y^*₁, y^*₂, …, y^*_n, как можно более близки к табличным значениям y₁, y₂,…, y_n.

Графически эту задачу можно представить следующим образом. В облаке точек x_i, y_i на плоскости x, y требуется провести плавную