1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
1.1 Определители
ОПР: Определителем второго порядка
называется число, обозначаемое: 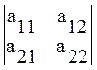 .
.
ВЫЧИСЛЕНИЕ: 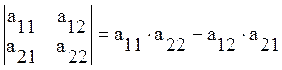 .
.
ПРИМЕР: Вычислить определитель второго порядка:
|
а) |
|
|
б) |
|
|
в) |
|
 ОПР: Определитель третьего порядка – это
число:
ОПР: Определитель третьего порядка – это
число:
|
|
|

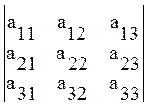
|
 ВЫЧИСЛЕНИЕ:
ВЫЧИСЛЕНИЕ:
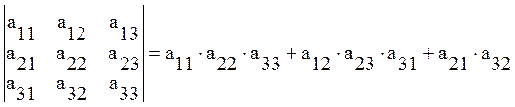 *
*
* ![]() .
.
ПРИМЕР: Вычислить определитель третьего порядка:
|
а) |
|
|
|
|
|
б) |
|
|
|
УПРАЖНЕНИЯ:
|
а) |
|
|
|
б) |
|
|
|
в) |
|
|
|
г) |
|
|
1.2 Формулы Крамера
Дана линейная неоднородная система ![]() алгебраических уравнений с
алгебраических уравнений с ![]() неизвестными (
неизвестными (![]() )
)
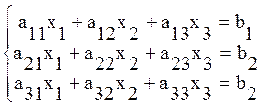 , где:
, где: ![]() ,
, ![]() ,
,
![]() – неизвестные;
– неизвестные; ![]() – коэффициенты уравнения;
– коэффициенты уравнения;
![]() ,
,
![]() ,
, ![]() –
свободные члены.
–
свободные члены.
ОПР: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы.
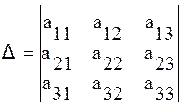
ОПР: ![]() ,
,
![]() ,
, ![]() –
определители, составленные из главного определителя системы заменой столбца
коэффициентов при неизвестных
–
определители, составленные из главного определителя системы заменой столбца
коэффициентов при неизвестных ![]() столбцом
свободных членов.
столбцом
свободных членов.
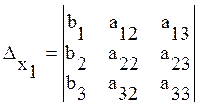 .
.
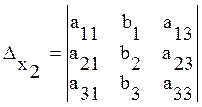 .
.
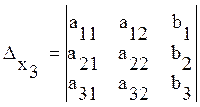 .
.
ТЕОРЕМА: Если главный определитель
системы ![]() линейных неоднородных
уравнений с
линейных неоднородных
уравнений с ![]() неизвестными отличается от
нуля, то система совместна.
неизвестными отличается от
нуля, то система совместна.
Решение этой системы можно найти по формулам Крамера:
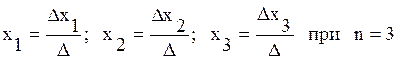 .
.
ПРИМЕР: Решить систему по формулам Крамера:
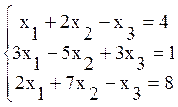 .
.
РЕШЕНИЕ:
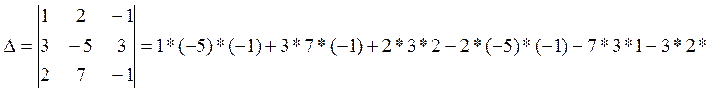
![]() система
совместна;
система
совместна;
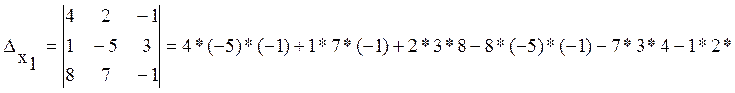
![]() ;
;
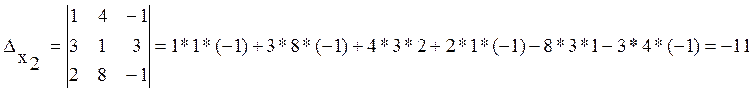 ;
;
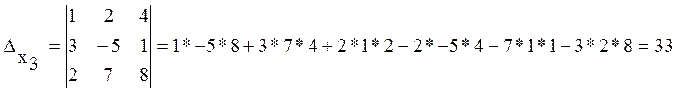 .
.
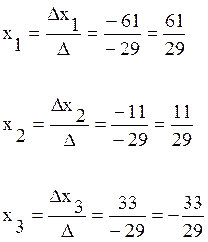
Ответ: 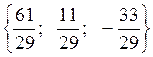 .
.
УПРАЖНЕНИЯ: Решить систему по формулам Крамера
|
|
|
1.3 Геометрические векторы
 ОПР: Геометрическим вектором называется
направленный отрезок прямой
ОПР: Геометрическим вектором называется
направленный отрезок прямой
ОБОЗНАЧЕНИЕ: ![]() или
или
![]() , точка A –
начало вектора, точка B – конец
вектора.
, точка A –
начало вектора, точка B – конец
вектора.
ОПР: Длиной отрезка AB называется длина (модуль) вектора ![]() .
.
ОБОЗНАЧЕНИЕ: ![]() или
или
![]() ,
,
ОПР: Векторы называются компланарными, если они принадлежат одной плоскости или параллельным плоскостям.
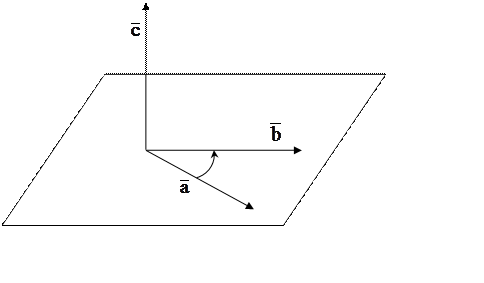 ОПР: Тройка векторов
ОПР: Тройка векторов ![]() называется правой, если
смотря из конца третьего вектора
называется правой, если
смотря из конца третьего вектора ![]() кратчайший
поворот от первого вектора
кратчайший
поворот от первого вектора ![]() ко второму
ко второму
![]() будет виден как движение
против часовой стрелки.
будет виден как движение
против часовой стрелки.
Если движение видно по часовой
стрелке, то тройка векторов ![]() называется
левой.
называется
левой.
ОПР: Модуль вектора равен квадратному корню из суммы квадратов его координат.
Если 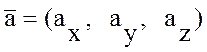 ,
то
,
то 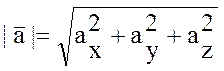 .
.
ПРИМЕР: Найти длину вектора.
|
1) |
|
|
2) |
Вектор имеет координаты
|
|
3) |
Вектор имеет координаты
|
ОПР: Если вектор ![]() , где
, где ![]() и
и ![]() , то:
, то:
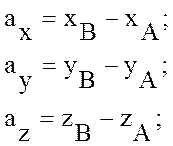
![]() .
.
ПРИМЕР: Даны точки ![]() и
и ![]() . Найти расстояние между
двумя точками
. Найти расстояние между
двумя точками ![]() и
и ![]() .
.
РЕШЕНИЕ: Рассмотрим вектор ![]() , по формуле:
, по формуле:
![]() ;
;
![]() .
.
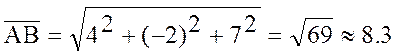
1.4 Линейные операции над векторами
1. Сложение векторов
Если 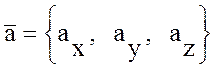 ,
, 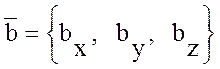 , то
, то 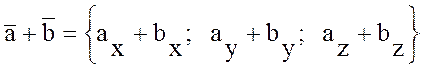 ;
;
2. Вычитание векторов
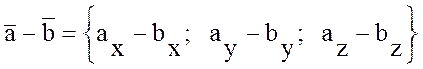
3. Умножение вектора на скаляр
Если 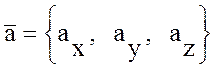 ,
, ![]() – число, то
– число, то
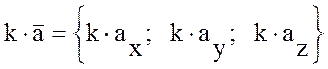 .
.
ПРИМЕР:
Даны: ![]() ,
,
![]() ,
, ![]() .
.
Найти:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() .
.
РЕШЕНИЕ:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ,
,
![]() ;
;
6) ![]() ,
,
![]() ,
,
![]() ;
;
УПРАЖНЕНИЯ: Даны точки ![]() ,
, ![]() ,
,
![]() . Найти:
. Найти:
|
1) |
|
|
|
2) |
|
|
|
3) |
|
|
|
4) |
|
|
|
5) |
|
|
|
6) |
|
|
|
7) |
|
|
|
8) |
|
|
1.5 Скалярное произведение двух векторов
ОПР: Скалярным произведением вектора ![]() на
на ![]() называется число, равное
произведению их модулей на косинус угла между ними.
называется число, равное
произведению их модулей на косинус угла между ними.
![]() ОБОЗНАЧЕНИЕ:
ОБОЗНАЧЕНИЕ: ![]() .
.
Свойства скалярного произведения:
1. ![]() ;
;
2. ![]() ;
;
3. ![]()
4. ![]() –
скалярный квадрат вектора равен квадрату его модуля;
–
скалярный квадрат вектора равен квадрату его модуля;
5. ![]()
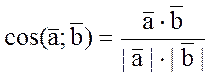 ;
;
6. Условие ортогональности двух
векторов ![]() и
и ![]() : Если
: Если ![]() и
и ![]() – ненулевые, то их скалярное
произведение равно нулю тогда и только тогда, когда эти векторы ортогональны:
– ненулевые, то их скалярное
произведение равно нулю тогда и только тогда, когда эти векторы ортогональны: ![]() ;
;
7. Скалярное произведение в
координатной форме: Если векторы заданы своими координатами 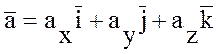 и
и 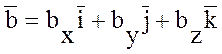 , то
, то 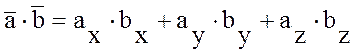 . Скалярное произведение двух
векторов равно сумме произведений их одноименных координат.
. Скалярное произведение двух
векторов равно сумме произведений их одноименных координат.
Геометрический смысл скалярного произведения:
![]() ПРИМЕР: Найти скалярное произведение
векторов, если
ПРИМЕР: Найти скалярное произведение
векторов, если ![]() ;
; ![]() ;
; ![]() .
.
![]() РЕШЕНИЕ: По определению скалярного
произведения
РЕШЕНИЕ: По определению скалярного
произведения ![]()
![]() ,
то
,
то 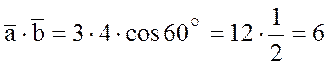 .
.
ПРИМЕР: Найти скалярное
произведение векторов, если ![]() ;
; ![]() .
.
РЕШЕНИЕ: По свойству №7 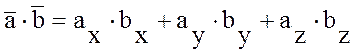 получим
получим ![]() .
.
ПРИМЕР: Доказать что векторы ![]() и
и ![]() ортогональны, если
ортогональны, если ![]() ;
; ![]() .
.
РЕШЕНИЕ: По свойству №6 ![]() , если
, если ![]() ,
, ![]() векторы не являются
ортогональными.
векторы не являются
ортогональными.
ПРИМЕР: Найти угол между двумя
векторами ![]() и
и ![]() , если
, если ![]() ;
; ![]() ;
;
![]() .
.
![]() РЕШЕНИЕ: По свойству №5
РЕШЕНИЕ: По свойству №5 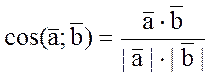 ,
, 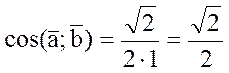 ,
,
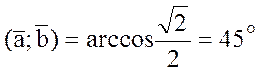 .
.
![]() ПРИМЕР: Найти скалярное произведение
ПРИМЕР: Найти скалярное произведение ![]() , если
, если ![]() ;
; ![]() ;
;
![]() .
.
РЕШЕНИЕ: По определению скалярного
произведения и свойству №3 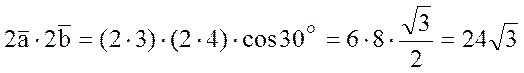
![]() ПРИМЕР: Найти
ПРИМЕР: Найти ![]() ,
если
,
если ![]() , если
, если ![]() ;
; ![]() ;
;
![]() .
.
![]() РЕШЕНИЕ: По геометрическому смыслу
скалярного произведения
РЕШЕНИЕ: По геометрическому смыслу
скалярного произведения 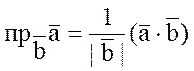 , по
определению скалярного произведения
, по
определению скалярного произведения ![]() ,
, 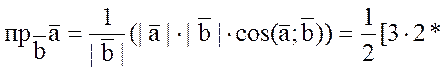
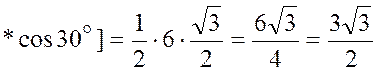 .
.
УПРАЖНЕНИЯ:
|
1) |
Доказать, что векторы ортогональны, если
|
|
|
2) |
|
|
|
3) |
|
|
|
4) |
Найти угол между |
|
|
5) |
Найти |
|
|
6) |
Найти скалярное произведение
|
|
1.6 Векторное произведение
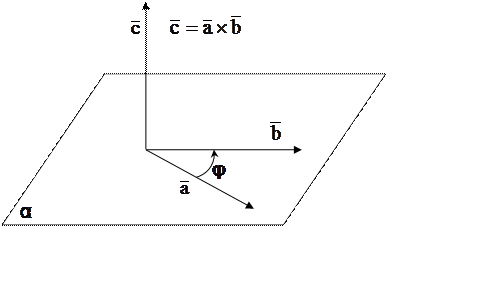
ОПР: Векторным произведением вектора ![]() на вектор
на вектор ![]() называется такой вектор
называется такой вектор ![]() , который удовлетворяет
условиям:
, который удовлетворяет
условиям:
1) его модуль численно равен площади
параллелограмма, построенного на векторах ![]() и
и
![]() как на сторонах;
как на сторонах;
2) ![]() и
и
![]() ;
;
3) тройка ![]() –
правая
–
правая
ОБОЗНАЧЕНИЕ: ![]()
![]() .
.
 |
Свойства векторного произведения:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) Условие коллинеарности двух векторов:
Векторное произведение равно
нуль–вектору тогда и только тогда, когда векторы коллинеарны ![]() , то
, то ![]() | |
| |![]() , если
, если ![]() ,
, ![]() ;
;
5) Векторное произведение в координатной форме:
Если 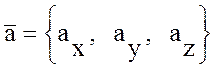 ,
,
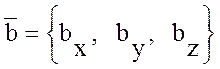 , то
, то
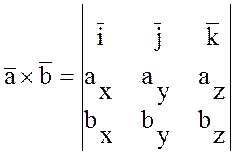 .
.
Геометрический смысл векторного произведения:
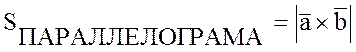 и
и  .
.
ПРИМЕР: Найти модуль векторного
произведения ![]() , если
, если ![]() ;
; ![]() ;
;
![]() .
.
РЕШЕНИЕ: По определению векторного
произведения 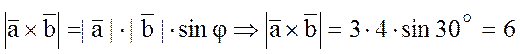 .
.
ПРИМЕР: Найти площадь
параллелограмма построенного на векторах ![]() и
и
![]() как на сторонах, если
как на сторонах, если ![]() ;
; ![]() ;
;
![]() .
.
РЕШЕНИЕ:
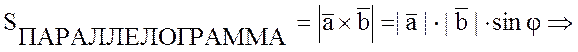
 .
.
ПРИМЕР: Найти ![]() , если
, если ![]() ,
, ![]() .
.
РЕШЕНИЕ: По свойству №5
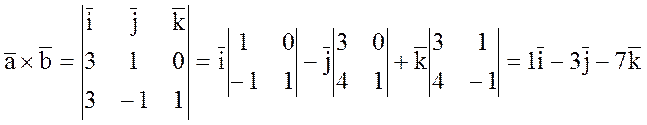 ,
,
![]() .
.
УПРАЖНЕНИЯ:
|
1) |
Найти |
|
|
2) |
Найти |
|
|
3) |
Найти |
|
|
4) |
Найти |
|
|
5) |
Доказать, что векторы коллинеарны, если
|
|
1.7 Смешанное произведение трех векторов
ОПР: Смешанным произведением трех векторов называется их векторно–скалярное произведение.
ОБОЗНАЧЕНИЕ: ![]() или
или
![]()
Геометрический смысл векторного произведения:
Произведение трех векторов равно объему параллелепипеда, построенного на векторах как на ребрах, со знаком «+», если тройка правая, и со знаком «–», если тройка левая.
![]() .
.
Свойства смешанного произведения:
1) ![]() ;
;
2) ![]() ;
;
3) Условие компланарности трех векторов:
Три вектора компланарные тогда и
только тогда, когда их смешанное произведение равно нулю. ![]() ;
;
4) Вычисление смешанного произведения в координатной форме:
Если 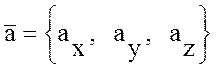 ,
,
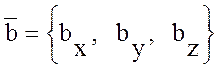 ,
, 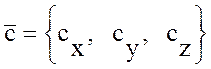 ,
то
,
то
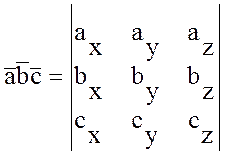 ;
;
5) Объем пирамиды: 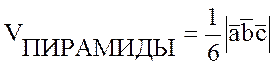 .
.
ПРИМЕР: Найти смешанное
произведение ![]() , если
, если ![]() ,
, ![]() ,
,
![]() .
.
РЕШЕНИЕ: по свойству №4:
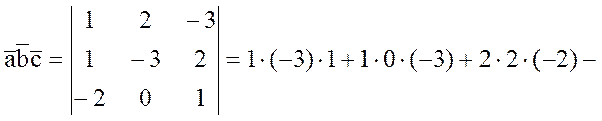
![]() .
.
ПРИМЕР: Доказать, что ![]() – компланарные, если
– компланарные, если ![]() ,
, ![]() ,
,
![]() .
.
РЕШЕНИЕ: по свойству №3:
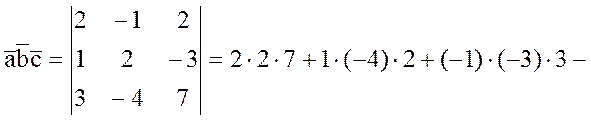
![]() векторы
копланарные.
векторы
копланарные.
УПРАЖНЕНИЯ:
Даны: ![]() ,
, ![]() ,
, ![]() .
.
|
1) |
Найти смешанное произведение |
|
|
2) |
Установить компланарность |
|
|
3) |
Найти объем параллелепипеда |
|
|
4) |
Найти объем пирамиды |
|
|
5) |
Установить вид тройки векторов |
|
2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
2.1 Прямая на плоскости
Если на плоскости задана декартова
система координат, то прямую на плоскости можно задать как линию пересечения
плоскостей ![]() и
и ![]() , т.е. уравнением:
, т.е. уравнением:
1. Общее уравнение прямой на
плоскости: ![]() ;
;
2. Уравнение прямой в отрезках: 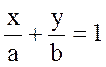 ;
;
3. Уравнение прямой, проходящей
через две точки ![]() и
и ![]() :
: 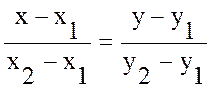
4.  Если известны угловой коэффициент
прямой
Если известны угловой коэффициент
прямой ![]() , и
, и ![]() – отрезок, отсекаемый на оси
– отрезок, отсекаемый на оси
![]() , то уравнение прямой с
угловым коэффициентом имеет вид:
, то уравнение прямой с
угловым коэффициентом имеет вид: ![]() .
.
Если ![]() ,
то уравнение прямой имеет вид
,
то уравнение прямой имеет вид ![]() и прямая
параллельна
и прямая
параллельна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.