Министерство образования РФ
Ижевский государственный технический университет
Кафедра «Программное обеспечение»
Выполнил :
Студент группы 4-19-1
Принял :
1. ПОСТАНОВКА ЗАДАЧИ
Задание 1: Определить с точностью ![]() значение решения задачи Коши в выбранной точке b.
Варианты задания:
значение решения задачи Коши в выбранной точке b.
Варианты задания:
а.) Составить процедуру численного решения задачи Коши для уравнения: 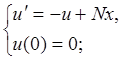 , где N=6.
, где N=6.
b.) Применить задание а для вычисления решения
задачи Коши для уравнения: 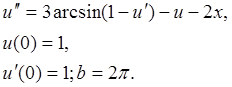
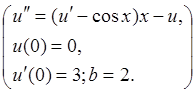
Задание 2: Используя метод конечных разностей, составить решение
краевой задачи для обыкновенного дифференциального уравнения с точностью ![]() , шаг h=0.1:
, шаг h=0.1:
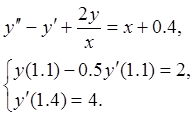
2. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Пусть дана система дифференциальных уравнений:
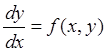 (1)
(1)
и начальные условия y(x0)=y0.
Задавшись некоторым шагом h и введя стандартные обозначения xi=x0+ih и yi=yi(xi), Dyi=yi+1-yi при i=0, 1, 2, …, положим:
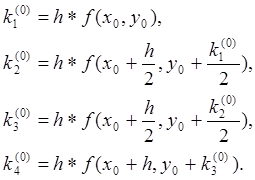 (2)
(2)
Согласно методу Рунге-Кутта Dy0 приближенно определяют по формуле
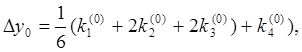 (3)
(3)
отсюда y1=y0+Dy0.
Далее, приняв (x1, y1) за исходные данные и повторяя тот же процесс, находим y2. Аналогично вычисляются yi (i=3, 4,…).
Имея дифференциальное уравнение второго порядка, положим u’=w, а следовательно w’=u’’. Отсюда распишем уравнение в виде системы:
f=[u’, w’], k=[k(1), k(2)],
где u’=w, w’ в нашем задании w’=–w2–u+ln x и компоненты k(1) и k(2) определяются из формул (2).
За абсолютную погрешность приближенного решения, вычисленную по методу Рунге-Кутта k-ого порядка, принимается
R=|(y1-y2)/(2k-1)|.
Если R<=E, то шаг h уменьшается в два раза, и вычисления повторяются, исходя из узла x0. Как только на очередном этапе будет получено R<E, считается, что y2 и является решением в узле x1=x0+h, полученным с заданной точностью E на этом шаге.
Решение в следующем узле x2, исходя из узла x1, получается аналогичным образом. При этом начальный шаг выбирается по шагу h, с которым было получено решение в узле x1, в зависимости от погрешности R: если R<E/2k+1, то предыдущий шаг удваивается; в противном случае шаг не изменяется. Аналогично находится решение и в последующих узлах.
При подходе к точке x=b следует проявлять осторожность. Если D=b-xk окажется меньше E1=E*0.1, то можно считать, что xk » bи на этом процесс интегрирования заканчивается. При D>=E1 интегрирование должно быть продолжено. Если при этом h<=D, то очередной этап не выводит за пределы интегрирования, и он делается обычным образом. Если же h>D, то в качестве h следует взять величину D.
Алгоритм для нахождения решения задачи Коши методом Рунге-Кутта:
1. x ::= a1; y ::= y01; h::=0.1; eps::=0.0001; i::=0;
2. k1 ::= h * f1(x, y);
k2 ::= h * f1(x + h/2, y + k1/2);
k3 ::= h * f1(x + h/2, y + k2/2);
k4 ::= h * f1(x + h, y + k3);
y ::= y + (k1 + 2*k2 + 2*k3 + k4)/6;
x ::= x + h;
i ::= i + 1;
3. Если (|b1-x| < eps*0.1), то переход к п., иначе к п.4;
4. rc4 ::=y;
5. y_New ::= rc4;
6. y_Old ::= y_New;
h ::= h/2 ;
7. y_New := rc41; переход к п.2;
8. Если (|(y_Old - y_New)/k| < eps), то переход к п.9, иначе к п.6;
9. Конец;
3. ТЕСТИРОВАНИЕ
Тексты программы приведены в приложении 1.
3.1. Тестирование программы VM43.CPP
Программа содержит процедуры реализующие вычисление решения краевой задачи для обыкновенного дифференциального уравнения, решения задачи Коши для дифференциального уравнения первого порядка и решения задачи Коши для дифференциального уравнения второго порядка.
Результаты работы программы:
Метод Рунге-Кутта 41 : 30.0148725
Точное значение : 30.0148725
Точность вычислений : 0.0001000
Количество итераций : 120
------------------------------------------Метод Рунге-Кутта 21 : 30.0149112
Точное значение : 30.0148725
Точность вычислений : 0.0001000
Количество итераций : 120
------------------------------------------Метод Рунге-Кутта 42 : 4.9092973
Точность вычислений : 0.0001000
Количество итераций : 40
------------------------------------------Метод Рунге-Кутта 32 : 4.9092669
Точность вычислений : 0.0001000
Количество итераций : 40
------------------------------------------Решение краевой задачи : 0.7850480
Точность вычислений : 0.0010000
Количество итераций : 4
------------------------------------------По результатам работы программы показывают, что в процедуре, реализующей вычисление решения задачи Коши методом Рунге-Кутта-4 выполняется меньшее количество итераций, чем в методе Рунге-Кутта-2 (можно пронаблюдать при изменении шага).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.