Комплексному числу ![]() соответствует
показательная форма записи
соответствует
показательная форма записи
![]() ;
;
14 Комплексному числу –1–j соответствует показательная форма записи
![]() .
.
15 Комплексному числу –3j соответствует показательная форма записи
3![]() ;
;
16 Комплексному числу 1+j соответствует тригонометрическая форма записи
![]() (cos
(cos![]() +j
sin
+j
sin![]() );
);
17 Комплексному числу ![]() соответствует
тригонометрическая форма записи
соответствует
тригонометрическая форма записи
![]() (cos
(cos![]() +j
sin
+j
sin![]() ).
).
18 Комплексному числу 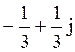 соответствует
тригонометрическая форма записи
соответствует
тригонометрическая форма записи
![]() (cos
(cos![]() +j
sin
+j
sin![]() );
);
19 Комплексному числу ![]() соответствует
тригонометрическая форма записи
соответствует
тригонометрическая форма записи
![]() (cos
(cos![]() –j sin
–j sin![]() );
);
20 Сумма комплексных чисел 2+j и –4–3j равна
–2–2j;
21 Разность комплексных чисел –j и 1+4j равна
–1–5j.
22 Произведение
комплексных чисел ![]() и
и
![]() равно
равно
-6j;
23 Произведение комплексных чисел ![]() и
2+j равно
и
2+j равно
–![]() +2
+2![]() j.
j.
24 Сумма комплексных чисел 7+3j и –4+2j равна
3+5j;
25 ![]() , z3 равно 16
, z3 равно 16![]() ;
;
26 z=1+j, z4 равно 4eπj;
27 ![]() , z6 в тригонометрической форме равно 8 (cos
, z6 в тригонометрической форме равно 8 (cos![]() π+j sin
π+j sin![]() π);
π);
28 z=2 (cos![]() +jsin
+jsin![]() ) , z5 равно 32
(cos
) , z5 равно 32
(cos![]() +j sin
+j sin![]() ).
).
29 Точка А(1,–2) принадлежит прямой
4x+3y+2=0;
30Точка B(0,1/2) принадлежит прямой
5x+2y–1=0;
31 Точка C(–5,2) принадлежит прямой
x–2y+9=0;
32 Точка D(3,–2) принадлежит прямой
–4x–5y+2=0.
33
Точка F(![]() ,–1)
принадлежит прямой
,–1)
принадлежит прямой
4x–5y–7=0;
34 Прямая 8x–y+3=0 проходит через точку
D(–1,–5).
35 Прямая x–5y–1=0 проходит через точку
B(1,0);
36 Прямая –2x+3y–4=0 проходит через точку
C(–1/2,1);
37 Прямая 5x+3y–2=0 проходит через точку
B(–2,4);
38 Прямая –x–2y+7=0 проходит через точку
C(3,2);
39 Прямые заданы своими
уравнениями: l1: y=2x+3; l2: y= –2x+2; l3: y=![]() x–2; l4: y=2x–3,5. Из них
x–2; l4: y=2x–3,5. Из них
параллельны l1 и l4;
40 Прямые заданы своими
уравнениями: l1: y=![]() x+2; l2: y= 8x–3; l3: y=–8x+3; l4: y=8x+5. Из них
x+2; l2: y= 8x–3; l3: y=–8x+3; l4: y=8x+5. Из них
параллельны l2 и l4.
41 Прямые заданы своими
уравнениями: l1: y=4x+7; l2: y= –4x–3,5; l3: y=![]() x––3,5; l4: y=
–4x+7. Из них параллельны
x––3,5; l4: y=
–4x+7. Из них параллельны
l2 и l4;
42 Прямые заданы своими
уравнениями: l1: y=7x+5; l2: y=![]() x+5; l3: y=–7x+5; l4: y=7x–2. Из них параллельны
x+5; l3: y=–7x+5; l4: y=7x–2. Из них параллельны
l1 и l4.
43
Прямые
заданы своими уравнениями: l1: y=
–![]() x–2,5;
x–2,5;
l2: y=2x+1; l3: y=![]() x+3; l4: y= –
x+3; l4: y= –![]() x+1. Из них параллельны l1 и l4;
x+1. Из них параллельны l1 и l4;
44 Прямые заданы своими уравнениями: l1: y=2x+17;
l2: y= –2x+11; l3: y=![]() x+8; l4: y=x+17. Из них перпендикулярны: l2
и l3;
x+8; l4: y=x+17. Из них перпендикулярны: l2
и l3;
44
Прямые
заданы своими уравнениями: l1: y=
–5x–5; l2: y=5x+5; l3: y=![]() x–1; l4: y=1,5x–1. Из них
x–1; l4: y=1,5x–1. Из них
перпендикулярны: l1 и l3;
46 Прямые заданы своими уравнениями: l1: y=2x–4; l2: y=4x–2;
l3: y=![]() x+2; l4: y= –
x+2; l4: y= –![]() x +3. Из них перпендикулярны: l2
и l4.
x +3. Из них перпендикулярны: l2
и l4.
47 Прямые заданы своими уравнениями: l1: y=1,5x–2,5;
l2: y= –5x+2; l3: y=5x–2; l4: y=![]() x –3. Из них перпендикулярны l2
и l4;
x –3. Из них перпендикулярны l2
и l4;
48 Прямые заданы своими
уравнениями: l1: y=![]() x–17;
x–17;
l2: y= –![]() x+10; l3: y= = –
x+10; l3: y= = –![]() x+10; l4: y=
x+10; l4: y=![]() x –12. Из них перпендикулярны: l3 и l4;
x –12. Из них перпендикулярны: l3 и l4;
49 Прямые x–y+2=0 и 2x–y–3=0пересекаютсяв точке с координатами (5,7);
50 Прямые x+y=0 и 7x–4y=0 пересекаются в точке с координатами (0,0);
51 Прямые –3x–y+1=0 и 2x+y–1=0 пересекаются в точке с координатами (0,1).
52 Прямые 2x–5y+6=0 и –3x+3y=0 пересекаются в точке с координатами(2,2).
53 Прямые x+2y–7=0 и –x–8y–5=0 пересекаются в точке с координатами (11,–2);
54 Расстояние от точки А(1,1) до прямой 3x+4y+3=0 равно 2;
55 Расстояние от точки А(1,0) до прямой –3x+4y–2=0 равно 1;
56 Расстояние от точки B(0,0) до прямой –3x–4y+15=0 равно 3;
57 Расстояние от точки C(1,2) до прямой 3x–4y+5=0 равно 0.
58 ![]() =3,
=3, ![]() =4,
=4,
![]() =60ْ
. Скалярное произведение
=60ْ
. Скалярное произведение ![]() равно
6;
равно
6;
59 ![]() =2,
=2, ![]() =1,
=1,
![]() =45ْ
. Скалярное произведение
=45ْ
. Скалярное произведение ![]() равно
равно
![]() ;
;
60 ![]() =3,
=3, ![]() =5,
=5,
![]() =60ْ
. Скалярное произведение
=60ْ
. Скалярное произведение ![]() равно
30;
равно
30;
61 ![]() =2,
=2, ![]() =4,
=4,
![]() =30ْ
. Скалярное произведение
=30ْ
. Скалярное произведение 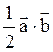 равно
2√ 3
равно
2√ 3
62 ![]() =5,
=5, ![]() =7,
=7,
![]() =90ْ
. Скалярное произведение
=90ْ
. Скалярное произведение ![]() равно
0.
равно
0.
63 ![]() =3,
=3, ![]() =4,
=4,
![]() =60ْ
.
=60ْ
. ![]() равно
равно ![]() ;
;
64 ![]() =2,
=2, ![]() =3,
=3,
![]() =45ْ
.
=45ْ
. ![]() равно
равно![]() ;
;
65 ![]() =3,
=3, ![]() =1,
=1,
![]() =30ْ
.
=30ْ
. ![]() равно 3
равно 3![]() ;
;
66 ![]() =4,
=4, ![]() =2,
=2,
![]() =60ْ
.
=60ْ
. ![]() равно 1;
равно 1;
67 ![]() =1,
=1, ![]() =3,
=3,
![]() =90ْ
.
=90ْ
. ![]() равно 0;
равно 0;
68 ![]() (1,1,1),
(1,1,1), ![]() (0,1,0),
(0,1,0), ![]() (–1,2,–3). Координаты вектора
(–1,2,–3). Координаты вектора
![]() :
(0,4,–2);
:
(0,4,–2);
69 ![]() (1,0,0),
(1,0,0), ![]() (1,2,2), λ=3. Координаты вектора
(1,2,2), λ=3. Координаты вектора ![]() : (2,–2,–2);
: (2,–2,–2);
70 ![]() (0,1,0),
(0,1,0), ![]() (1,1,0),
(1,1,0), ![]() (0,1,1). Координаты вектора :
(0,1,1). Координаты вектора : ![]() : (1,0,–2);
: (1,0,–2);
71 ![]() (–1,–1,0),
(–1,–1,0), ![]() (0,1,1), λ=2, β=3. Координаты вектора
(0,1,1), λ=2, β=3. Координаты вектора ![]() :
(–2,1,3);
:
(–2,1,3);
72 ![]() (1,1,1),
(1,1,1), ![]() (2,2,1),
(2,2,1), ![]() (0,2,0). Координаты вектора
(0,2,0). Координаты вектора ![]() :
(3,11,2);
:
(3,11,2);
73 Длина вектора ![]() (1,2,–2) равна 3;
(1,2,–2) равна 3;
74 Длина вектора ![]() (0,–4,3) равна 5;
(0,–4,3) равна 5;
75 Длина вектора ![]() (4,0,–2) равна 2
(4,0,–2) равна 2![]() ;
;
76 Длина вектора ![]() (2,1,–2) равна 3;
(2,1,–2) равна 3;
77 Длина вектора ![]() (–1,4,1) равна 3
(–1,4,1) равна 3![]() ;
;
78 ![]() (–1,2,4),
(–1,2,4), ![]() (0,0,0),
(0,0,0), ![]() (1,–1,5). Смешанное произведение
(abc) равнo 0;
(1,–1,5). Смешанное произведение
(abc) равнo 0;
79 ![]() (–1,2,0),
(–1,2,0), ![]() (1,–2,0),
(1,–2,0), ![]() (2,1,0). Смешанное произведение
(abc) равнo 0.
(2,1,0). Смешанное произведение
(abc) равнo 0.
80 ![]() (0,0,1),
(0,0,1), ![]() (0,–2,0),
(0,–2,0), ![]() (1,0,0). Смешанное произведение
(abc) равнo2;
(1,0,0). Смешанное произведение
(abc) равнo2;
81 ![]() (1,0,0),
(1,0,0), ![]() (0,1,0),
(0,1,0), ![]() (0,0,2). Смешанное произведение
(abc) равнo 2;
(0,0,2). Смешанное произведение
(abc) равнo 2;
82 ![]() (–1,0,3),
(–1,0,3), ![]() (–2,0,1),
(–2,0,1), ![]() (4,0,–3). Смешанное произведение
(abc) равнo 0;
(4,0,–3). Смешанное произведение
(abc) равнo 0;
83 ![]() =1,
=1, ![]() =4,
=4,
![]() =30ْ
. Модуль векторного произведения
=30ْ
. Модуль векторного произведения ![]() равен
2.
равен
2.
84 ![]() =2,
=2, ![]() =1,
=1,
![]() =45ْ
. Модуль векторного произведения
=45ْ
. Модуль векторного произведения ![]() равен
равен
![]() ;
;
85 ![]() =5,
=5, ![]() =3,
=3,
![]() =90ْ
. Модуль векторного произведения
=90ْ
. Модуль векторного произведения ![]() равен
15;
равен
15;
86 ![]() =2,
=2, ![]() =4,
=4,
![]() =60ْ
. Площадь параллелограмма, построенного на векторах
=60ْ
. Площадь параллелограмма, построенного на векторах ![]() и
и
![]() как
на сторонах,
как
на сторонах,
равна 4![]() ;
;
87 ![]() =1,
=1, ![]() =2,
=2,
![]() =30ْ
. Площадь параллелограмма, построенного на векторах
=30ْ
. Площадь параллелограмма, построенного на векторах ![]() и
и
![]() как
на сторонах,
как
на сторонах,
равна 1.
88Точка А(2,0,0) принадлежит плоскости6x+5y–4z–12=0;
89Точка B(1,0,1) принадлежит плоскости3x+2y+z–4=0;
90Точка C(0,2,1) принадлежит плоскости5x–2y+z+3=0.
91Точка D(1,1,0) принадлежит плоскости2x+2y–4z–4=0;
92Точка F(–1,0,2) принадлежит плоскости3x+4y+z+1=0.
93 Координаты нормального вектора плоскости 3x+4y–6=0 : (3,4,0);
94 Координаты нормального вектора плоскости x+y–3z+8=0 : (1,1,–3);
95 Координаты нормального вектора плоскости –2x–3z+5=0 : (–2,0,–3).
96 Координаты нормального вектора плоскости 3y–4z–2=0 : (0,3,–4);
97 Координаты нормального вектора плоскости 5x+3y–7z–1=0 : (5,3,–7);
98 Плоскости заданы своими уравнениями: α: x+y+2z–1=0, β: 3x–2y–5z+4=0, j: 2x+2y+4z+3=0,
σ: –x 4y+7z+6=0. Их них параллельны:α и j;
99 Плоскости заданы своими уравнениями: α: –2x+2y–5z=0, β: 3x+y–2z–2=0, j: 4x–3y+6z+4=0, σ: 6x+2y–4z+1=0.
Их них параллельны: β и σ;
100 Плоскости заданы своими уравнениями: α: 3x–y–z+8=0, β: 3x–2y–2z+8=0, j: –7x–3y+6z+14=0,
σ: 9x–3y–3z–5=0. Их них параллельны: α и σ;
101 Плоскости заданы своими уравнениями: α: –x–y+6z=0, β: 2x–3y+5z+3=0, j: –x+2y–2z–4=0, σ: 2x–4y+4z+2=0.
Их них параллельны : j и σ.
102 Плоскости заданы своими уравнениями: α: 8x–7y+16z+4=0, β: 6x+4y–2z–2=0, j: –4x–3y+14z+3=0,
σ: 3x+2y–z+12=0. Их них параллельны : β и σ;
103 Плоскости заданы своими уравнениями: α: x–6y+2z+3=0, β: 3x–5z+4=0, j: 4x+y+z–2=0, σ: –7x+4y+8z+14=0.
Их них перпендикулярны : α и j;
104 Плоскости заданы своими уравнениями: α: 4x+y+8z–10=0, β: 3x–2y+6=0, j: –7x–5y+2z+1=0, σ: –2x–3y+z–3=0.
Их них перпендикулярны: σ и β.
105 Плоскости заданы своими уравнениями: α: 3x–y+8z+13=0, β: –x+2y––3z+1=0, j: 6x+2y–2z–4=0,
σ: 2x–5z+18=0. Их них перпендикулярны: α и j;
106 Плоскости заданы своими уравнениями: α: 8x+z–3=0, β: 3x–4y+z–2=0, j: 2x+y–2z+3=0, σ: –3x–6y+7=0. Их
них перпендикулярны β и j;
107 Прямые заданы своими уравнениями:
l1: 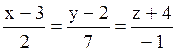 ; l2:
; l2: 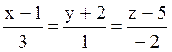 ;
;
l3: 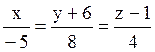 ; l4:
; l4: 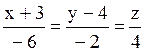 .
.
Из них параллельны : l2 и l4;
108 Прямые заданы своими уравнениями:
l1: 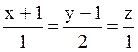 ; l2:
; l2: 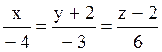 ;
;
l3: 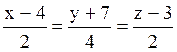 ; l4:
; l4: 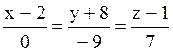 . Из них параллельны l1 и l3;
. Из них параллельны l1 и l3;
109 Прямые заданы своими уравнениями:
l1: 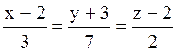 ; l2:
; l2: 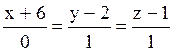 ;
;
l3: 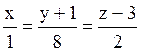 ; l4:
; l4: 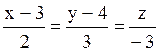 .
.
Из них перпендикулярны: l2 и l4;
110 Прямые заданы своими уравнениями:
l1: 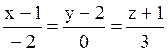 ; l2:
; l2: 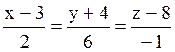 ;
;
l3: 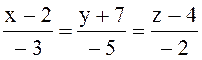 ; l4:
; l4: 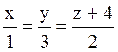 .
.
Из них перпендикулярны: l1 и l3;
111 Прямые заданы своими уравнениями:
l1: 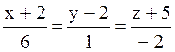 ; l2:
; l2: 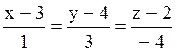 ;
;
l3: 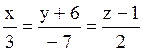 ; l4:
; l4: 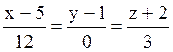 . Из них перпендикулярны l2 и l4.
. Из них перпендикулярны l2 и l4.
112 Прямая l и плоскости α, β, j,σ заданы своими уравнениями:
l: 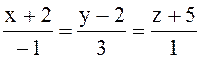 α: 4x–y+z–2=0, β: 5x+2y–z+4=0, j: –x+4y+3z+1=0, σ: 7x+y–8z–14=0.
α: 4x–y+z–2=0, β: 5x+2y–z+4=0, j: –x+4y+3z+1=0, σ: 7x+y–8z–14=0.
Прямая l параллельна плоскости : β;
113 Прямая l и плоскости α, β, j,σ заданы своими уравнениями:
l: 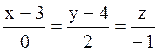 , α: 3x+7y+z–4=0, β: –2x–5y+3z+5=0, j: 4x+3y+6z–12=0, σ: –6x–y+4z–2=0.
, α: 3x+7y+z–4=0, β: –2x–5y+3z+5=0, j: 4x+3y+6z–12=0, σ: –6x–y+4z–2=0.
Прямая l параллельна плоскости: j;
114 Прямая l и плоскости α, β, j,σ заданы своими уравнениями:
l: 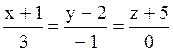 , α: 6x+y–3z+10=0, β: 4x+8y–7z+5=0, j: –2x–3y+5z–1=0, σ:
2x+6y–4z+3=0.
, α: 6x+y–3z+10=0, β: 4x+8y–7z+5=0, j: –2x–3y+5z–1=0, σ:
2x+6y–4z+3=0.
Прямая l параллельна плоскости: σ.
115 Прямая l и плоскости α, β, j,σ заданы своими уравнениями:
l: 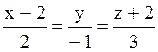 , α: 4x–2y+6z+11=0, β: –x+12y–3z+6=0, j: 2x+3y–4z+5=0, σ: –6x+4y+5z–2=0.
, α: 4x–2y+6z+11=0, β: –x+12y–3z+6=0, j: 2x+3y–4z+5=0, σ: –6x+4y+5z–2=0.
Прямая l перпендикулярна плоскостиα;
116 Прямая l и плоскости α, β, j,σ заданы своими уравнениями:
l: 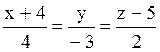 , α: –2x+4y–9z=0, β: –4x+3y–2z+5=0, j: 7x–y–3z+4=0, σ: x–3y+2z–10=0.
, α: –2x+4y–9z=0, β: –4x+3y–2z+5=0, j: 7x–y–3z+4=0, σ: x–3y+2z–10=0.
Прямая l перпендикулярна плоскости : β;
117 Прямая l и плоскости α, β, j,σ заданы своими уравнениями:
l: 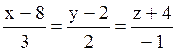 , α: –2x+3y–2=0, β: x+6y–z+1=0, j: 4x–z+3=0, σ: –6x–4y+2z–5=0
, α: –2x+3y–2=0, β: x+6y–z+1=0, j: 4x–z+3=0, σ: –6x–4y+2z–5=0
Прямая l перпендикулярна плоскости σ.
118 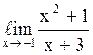 равен
1;
равен
1;
119 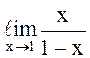 равен
¥.
равен
¥.
120 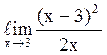 равен0;
равен0;
121 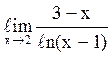 равен¥.
равен¥.
122 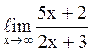 равен
равен![]() ;
;
123 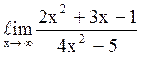 равен
равен![]() ;
;
124 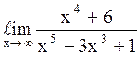 равен
0;
равен
0;
125 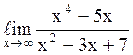 равен
¥.
равен
¥.
126 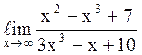 равен
–
равен
–![]() ;
;
127 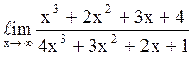 равен
равен ![]() ;
;
128 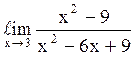 равен
¥.
равен
¥.
129 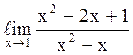 равен
0;
равен
0;
130 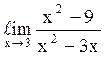 равен
2;
равен
2;
131 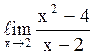 равен
4.
равен
4.
132 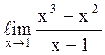 равен
1;
равен
1;
133 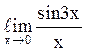 равен3;
равен3;
134 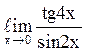 равен2;
равен2;
135 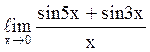 равен
8;
равен
8;
136 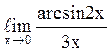 равен
равен
![]() .
.
137 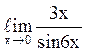 равен
½;
равен
½;
138 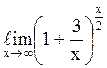 равен
равен![]() ;
;
139 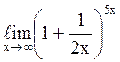 равен
равен![]() ;
;
140 ![]() равенe;
равенe;
141 ![]() равен
e8.
равен
e8.
142 ![]() равен
e –20.
равен
e –20.
143 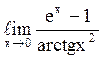 равен
¥.
равен
¥.
144 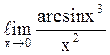 равен
0;
равен
0;
145 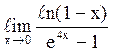 равен
равен ![]() ;
;
146 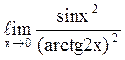 равен
равен
![]() ;
;
147 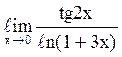 равен
равен ![]() ;
;
148 f(x)=2ex. Производная функции f(x) равна: 2ex;
149 f(x)=4arctgx. Производная функции f(x) равна
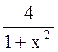 .
.
150 f(x)=![]() . Производная функции f(x)
равна: -
. Производная функции f(x)
равна: -![]() .
.
151 f(x)=3x5. Производная функции f(x) равна: 15x4;
152 f(x)=![]() . Производная функции f(x)
равна
. Производная функции f(x)
равна
–![]() sinx;
sinx;
153 f(x)=![]() . Производная функции f(x)
равна:
. Производная функции f(x)
равна: ![]() ;
;
154 f(x)=x+sinx. Производная функции f(x) равна
1+cosx;
155 f(x)=3x–lnx. Производная функции f(x) равна
3х–![]() ;
;
156 f(x)=arcsinx+arccosx. Производная функции f(x)
равна 0.
157 f(x)=ex+tgx. Производная функции f(x) равна
ex
+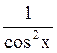 ;
;
158 f(x)=ax+x. Производная функции f(x) равна
axlna+1;
159 f(x)=shx–3x3. Производная функции f(x) равна
chx–9x2;
160 f(x)=ex·x. Производная функции f(x) равна
ex·x+ex;
161 f(x)=x·sinx. Производная функции f(x) равна
sinx+x·cosx;
162 f(x)=x·lnx. Производная функции f(x) равна
lnx+1.
163 f(x)=x2·ex. Производная функции f(x) равна
2xex+x2ex;
164 f(x)=sinx·cosx. Производная функции f(x) равна
cos2x–sin2x;
165 f(x)=x·tgx. Производная функции f(x) равна
tgx+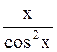 ;
;
166 f(x)=![]() . Производная функции f(x)
равна
. Производная функции f(x)
равна
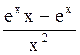 ;
;
167 f(x)=![]() . Производная функции f(x)
равна
. Производная функции f(x)
равна
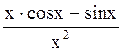 ;
;
168 f(x)=![]() . Производная функции f(x)
равна
. Производная функции f(x)
равна
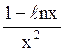 ;
;
169 f(x)=![]() . Производная функции f(x)
равна
. Производная функции f(x)
равна
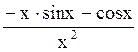 .
.
170 f(x)=![]() . Производная функции f(x)
равна
. Производная функции f(x)
равна
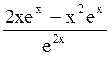 ;
;
171 f(x)=(x2–2)3. Производная функции f(x) равна
6x(x2–2)2;
172 f(x)=cos2x. Производная функции f(x) равна
–2cosx·sinx;
173 f(x)=esinx. Производная функции f(x) равна
cosx·esinx;
174 f(x)=ln(sinx). Производная функции f(x) равна
ctgx;
175 f(x)=sin![]() . Производная функции f(x)
равна
. Производная функции f(x)
равна
![]() cos
cos![]() ;
;
176 f(x)=![]() . Производная функции f(x)
равна
. Производная функции f(x)
равна
(3x2+2)![]() ;
;
177 f(x)=ln(x2+1). Производная функции f(x) равна
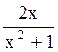 .
.
178 Функция y=x4–4x
убывает при x<1, возрастает при x>1;
179 Функция y=e2x всюду возрастает;
180 Функция y=lnx2
возрастает при x<0, убывает при x>0.
181 Функция y=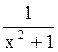
возрастает при x<0, убывает при x>0;
182 Функция y=![]()
возрастает при x>-1;
183 Функция f(x)=x4–x2–7 является четной;
184 Функция f(x)=x3+sinx является нечетной;
185 Функция f(x)=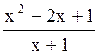 является общ. вида.
является общ. вида.
186 Функция f(x)=![]() является четной;
является четной;
187 Функция f(x)=x3–3x2+2x+5 является общ. вида.
188 Для функции y=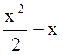 точкой min
является точка с координатами:
(1,-1/2);
точкой min
является точка с координатами:
(1,-1/2);
189 Для функции y=x6+6x точкой min является точка с координатами: (-1,-5);
190 Для функции y=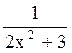 точкой
min является точка с координатами: (0,1/3);
точкой
min является точка с координатами: (0,1/3);
191 Горизонтальной
асимптотой графика функции y=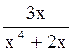 является
прямая: y=0;
является
прямая: y=0;
192 Горизонтальной
асимптотой графика функции y=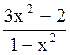 является
прямая: y= –3;
является
прямая: y= –3;
193 Функция y=x5+5x–6 : выпукла при x<0, вогнута при x>0;
194 Для функции y=x3–6x2+16 точкой перегиба является точка с координатами : (2,0).
195 Функция y=2x3+3 : выпукла при x<0, вогнута при x>0
196 Для функции y=5(x–1)3 точкой перегиба является точка с координатами: (1,0);
197 Область определения
функции y=![]() :
x³1 и x£–1;
:
x³1 и x£–1;
198 Для функции y=ln(x2+1) точкой min является точка с координатами: (0,0).
199 Для функции y=![]() точкой
max является точка с координатами : (1,1/e);
точкой
max является точка с координатами : (1,1/e);
200 Вертикальной
асимптотой графика функции y=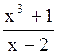 является
прямая
является
прямая
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.