Fтр= f*(T*sin(arctg (l/σ))+ G1*sinα)
- Динамический анализ.
T1= m1*V12/2= m1*(V1a)2= (m1* σ̉2+ V 2самолета при взлете+2* σ̉* V самолета при взлете)*0.5
П2= c*Δ2x= c*(L-L0)2
Qσ= (ΣWf)σ/σ̉= [m1*g*cosα+F* σ̉-T*σ̉*cos(arctg (l/σ)-Fтр*σ̉]/ σ̉= m1*g*cosα+F-T̉*cos(β)+ f*(T*sin(arctg (l/σ))+ m1*g*sinα)]
T= T1+П2= (m1* σ̉2+ V 2самолета при взлете+2* σ̉* V самолета при взлете)*0.5+ c*(L-L0)2
![]() =
= ![]() (m1*2* σ̉+2* V самолета при взлете)
(m1*2* σ̉+2* V самолета при взлете)
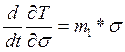 ״;
״;
m1*σ״![]() = m1*g*cos
= m1*g*cos![]() +F-T*cos(arctgl/σ)+f*(T*sin(arctgl/σ)+m1*g*sin
+F-T*cos(arctgl/σ)+f*(T*sin(arctgl/σ)+m1*g*sin![]()
σ״![]() g*cos
g*cos![]() +F*1/m1-T*cos(arctgl/σ)*1/m1+f*T*sin(arctgl/σ)*1/m1+g*sin
+F*1/m1-T*cos(arctgl/σ)*1/m1+f*T*sin(arctgl/σ)*1/m1+g*sin![]()
σ״=
g*(cos![]() +sin
+sin![]() )+F*1/m1-T/m1*[cos(arctgl/σ)+f*sin(arctgl/σ)]
)+F*1/m1-T/m1*[cos(arctgl/σ)+f*sin(arctgl/σ)]
Обозначим g*(cos![]() +sin
+sin![]() )+F*1/m1=А=const
)+F*1/m1=А=const
σ״= А-T/m1*[cos(arctgl/σ)+f*sin(arctgl/σ)]
Дальнейшее решение полученного дифференциального уравнения будем реализовывать двумя способами: аналитическим и численным методами.
2.4.2. Аналитический метод решения дифференциального уравнения.
AT-72= g*(cos![]() +sin
+sin![]() )+F*1/m=
10*(0.87+0.5)+342.5/44.5= 21.3
)+F*1/m=
10*(0.87+0.5)+342.5/44.5= 21.3
Aимт= 10*(0.87+0.5)+273.5/36=21.2
Aавтогрейдера 10*(0.87+0.5)+182.4/24= 21.2
Силы натяжения в тросе:
ТТ-72= 118кН; Tимт= 78кН; Tавтогрейдера 120кН.
σ״Т-72= 21.3-118/44.5*[cos(arctg2/σ)+0.3*sin(arctg2/σ)]= 21.3- 2.6*[cos(arctg2/σ+0.3*sin(arctg2/σ)]
σ׳T-72= 149.1-2.6*[7*cos(arctg2/σ)+2.1*sin(arctg2/σ)]= 149.1-18.2*cos(arctg2/σ)+5.46*sin(arctg2/σ),
σT-72= 1043.7-127.4*cos(arctg2/σ)+38.22*sin(arctg2/σ)=
1043.7-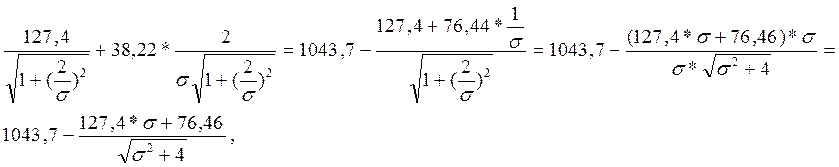 -σT-72+1043.7=
-σT-72+1043.7=
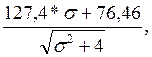
127.4*σ+76.46+σ*![]()
![]()
Полученное выражение возводим в квадрат:
(σ2+4)*(σ2-2*σ*1043,7+1043,72)= (127,4*σ)2+(76,46)2+2*127,4*76,46*σ.
Данное уравнение четвертого порядка решаем с помощью программы MathCad:
σ= 1,504 (м).
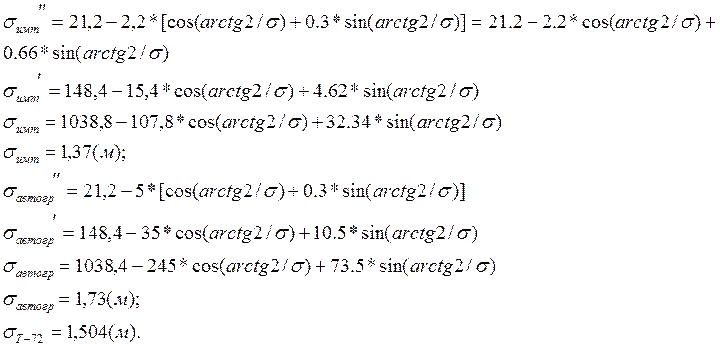
Выводы из полученных результатов.
- После взлета обобщенная координата σ для спец.изделия Т-72 измениться с 1,5 метров до 1,504 метра, что говорит о незначительном удлинении троса при взлете самолета;
- Обобщенная координата σ для спец.изделия ИМТ изменится с 1,37 метра до 1,375 метра;
- Обобщенная координата σ для спец.изделия автогрейдер изменится с 1,728 метра до 1,73 метра.
2.5. Расчет поперечных колебаний сильно натянутого троса.
Рассмотрим трос, натяжение которого Т значительно превосходит по модулю действующие на него силы, так что последними можно пренебречь. Очевидно, что такой трос, закрепленный в двух точках, принимает в положении равновесия форму прямой линии.
Рассмотрим поперечные колебания троса, считая, что каждая его точка М может перемещаться только в направлении, перпендикулярном равновесному положению, т.е. оси X (рисунок ).
Кроме того, будем предполагать, что поперечные перемещения U(x, t) всех точек троса лежат в одной плоскости и достаточно малы.
В соответствии с общей теорией малых колебаний
перемещения U и производные ![]() и
и ![]() считаются величинами
первого порядка малости.
считаются величинами
первого порядка малости.
Покажем, что в сделанных предположениях с точностью до членов высшего порядка малости при колебаниях троса его натяжение будет все время одинаково во всех точках.
Пусть dS и dS0=dx – длина элемента М1М2 троса в момент времени t и в положении равновесия соответственно. Тогда
dS= 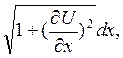
или, пренебрегая квадратом производной ![]() по сравнению с единицей,
по сравнению с единицей,
dS= dx= dS0.
Это означает, что при колебании троса растяжение с принятой точностью не изменяется и, следовательно, оно не вызывает с течением времени t изменения натяжения в рассматриваемой точке.
Составим теперь дифференциальные уравнения движения троса, учитывая, что в сделанных предположениях внешние силы равны нулю, колебания троса происходят в одной плоскости и что перемещения точек троса перпендикулярны оси x. Из последнего следует, что
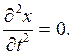
и, следовательно, имеем:
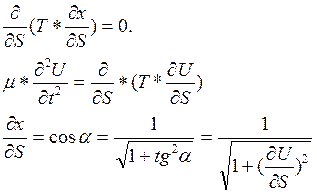
Так как, согласно установленному ранее, натяжение в точке М троса не зависит от времени t, то из равенства:
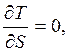
находим, что натяжение троса одинаково во всех точках, т.е. Т=Т0=const. Это полностью доказывает сделанное ранее утверждение.
Дифференциальное уравнение свободных поперечных колебаний троса:
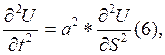
где постоянная величина a, имеющая размерность скорости, определена равенством:
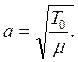
Уравнение (6), называемое волновым уравнением, должно удовлетворять двум начальным условиям и двум граничным условиям. Начальные условия имеют вид:
U= f(x);
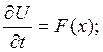
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.