Оценка возможности транспортировки специальных изделий воздушным транспортом. Транспортировка системы “носитель-трал” военно-транспортной авиацией, страница 4

В случае погрузки техники с применением откидной трап - рамы можно воспользоваться уровневой линейкой, устанавливаемой внутри грузовой кабины на ровную плоскую поверхность. Измеренный угол крена необходимо сравнить с допускаемым значением поперечной центровки (паспортная величина).

 

2.3.  Расчет сил натяжения в тросе.

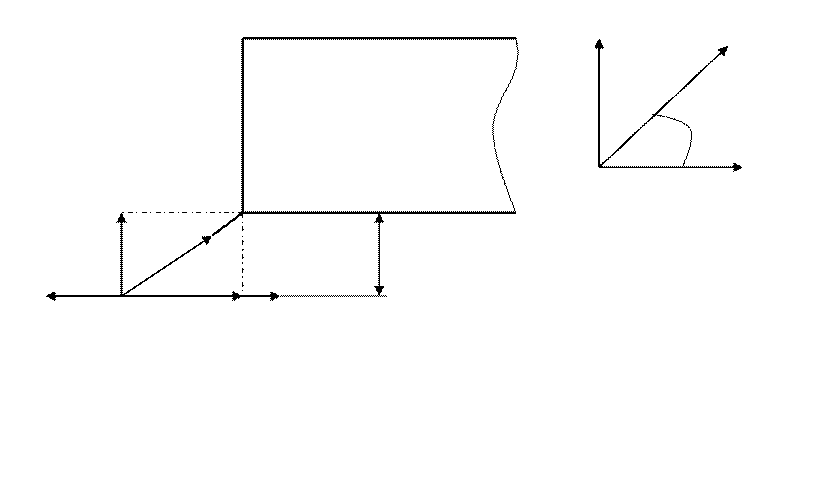                                                              Y

                                                                                                                  T

F_домк

X      z_{i                                                                                                     0}

α_i   l         T     β_i                  x_i

Y            

0             F_тр       Z

Рисунок 2.28  . Расчетная схема.

T_z*cosβ_i= F_тр^попер/4:

T_y*sinα_i= F_домк/4:

T_x*sinβ_i= F_тр^прод/4:

T_Σ=

Примем ряд допущений:

1.  груз будем считать симметричным;

2.  трением в шарнирах пренебрегаем;

3.  F_тр^поперF_тр^прод.

Примем:   x_i= 1 метр=1000мм;

длина троса l= 2000мм.

Определим величину sinα:

Z=

sinα= 1732/2000= 0.87;

cosβ=    

sinβ= x/l= 1000/2000=0.5;

cosβ= 0866.

F_тр= μ*N.

В нашем случае принимаем коэффициент трения μ= 0,3.

N= m*g.

N₁= m₁*g= 36*10³*9.8= 352.8*10³(H),

N₂= m₂*g= 24*10³*9.8= 235.2*10³(H),

N₃= m₃*g= 44.5*10³*9.8= 436.1*10³(H);

F_тр1= N₁*μ= 352.8*10³*0.3= 105.84(кН),

F_тр2= N₂*μ= 235,2*10³*0,3= 70,56(кН),

F_тр3= N₃*μ= 436.1*10³*0.3= 130.83(кН).

T_z1=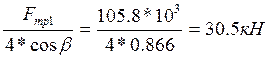

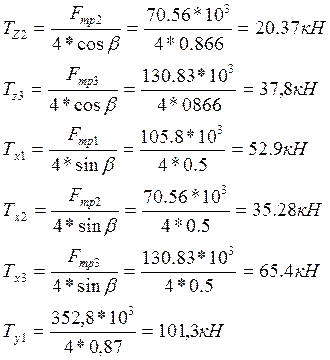
Т_у2=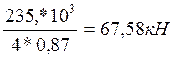

Т_у3=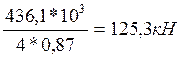

Определяем суммарное натяжение в тросе:

Т_Σ1=

Т_Σ2=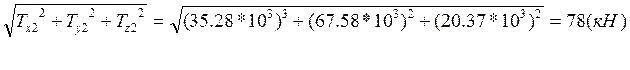

T_Σ3=

При растяжении каната:

σ_раст= T_Σi/F_сеч

В нашем случае [σ]= 220…230 МПа.

F_сеч=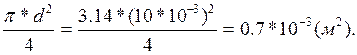

σ₁= 118*10³/0.7*10^-3=168.5*10⁶(Па),

σ₂= 79*10³/0,7*10^-3= 112,8*10⁶(Па),

σ₃= 120*10³/0,7*10^-3= 171,4*10⁶(Па).

Таким образом, можно сделать окончательный вывод о целесообразности применения данного типа канатов для закрепления груза в грузовом отсеке самолета, т.к.

σ_i<[σ].

 

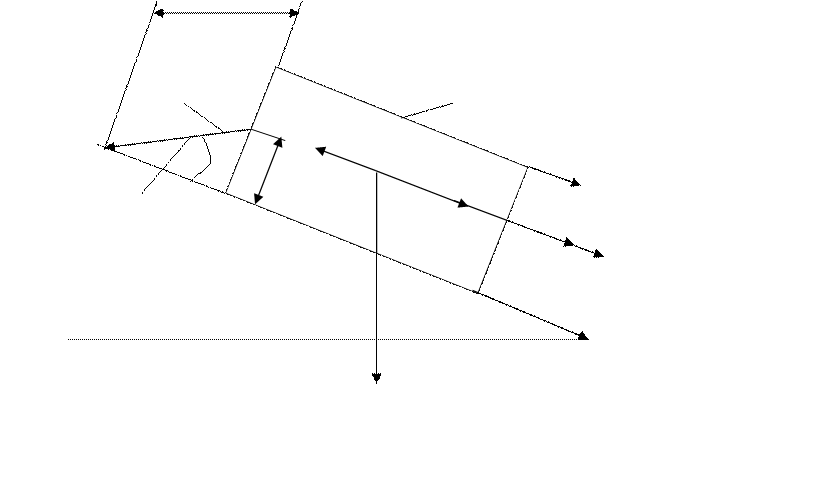
2.4. Исследование динамики модели системы “носитель-изделие-трос” при взлете самолета.

                                                  σ

L                      V₁^e                   1

T                      β        h         

2                                                                              F

V₁^a                V^a₁                                                                                             

x

F_тр

G₁

Рисунок     Динамическая модель системы “носитель-изделие-трос” при             взлете.

Уравнение Лагранжа 2 рода:

d/dt(  )-  =Q_j – это дифференциальное уравнение движения механической d системы в обобщенных координатах.

Полагаем, что связи, наложенные на систему, идеальные.

Получим эти уравнения, используя теорему:

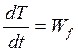
W_f – для системы с идеальными связями является суммой мощностей заданных сил.

В обобщенных координатах она определяется:

W_f=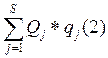

{Q_j}_s – обобщенные силы системы.

Для стационарной механической системы кинетическая энергия:

T= T{q_j, q̉_j}, поэтому

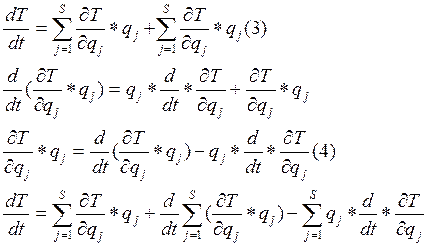
Так как кинетическая энергия стационарной механической системы является однородной квадратичной формой обобщенных скоростей { q̉_j}_s системы, то по теореме Эйлера для однородной функции имеем:

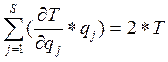
Теперь последнее равенство перепишем в виде:

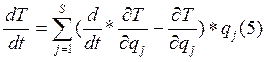
Подставляя (5) в (1)и учитывая (2) получим:

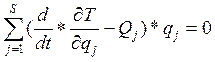
Отсюда, в силу независимости обобщенных скоростей { q̉_j}_s и получаем уравнение Лагранжа 2 рода.

2.4.1  Аналитические расчеты динамической модели.

Рассмотрим нашу систему, сделав движение изделие 1 сложным, связав подвижное пространство с грузовым полом самолета (рис. 2).

σ – обобщенная координата.

- Кинематический анализ.

V₁^e= V_{самолета при взлете};

V₁^r= σ̉;

V₁^a= V₁^e+ V₁^r;

Спроектируем все скорости на ось координат OX:

V₁^a= V₁^e- V₁^r= σ̉ - V_{самолета при взлете}.                                  

Рассмотрим равновесие груза 1:

                                                                     

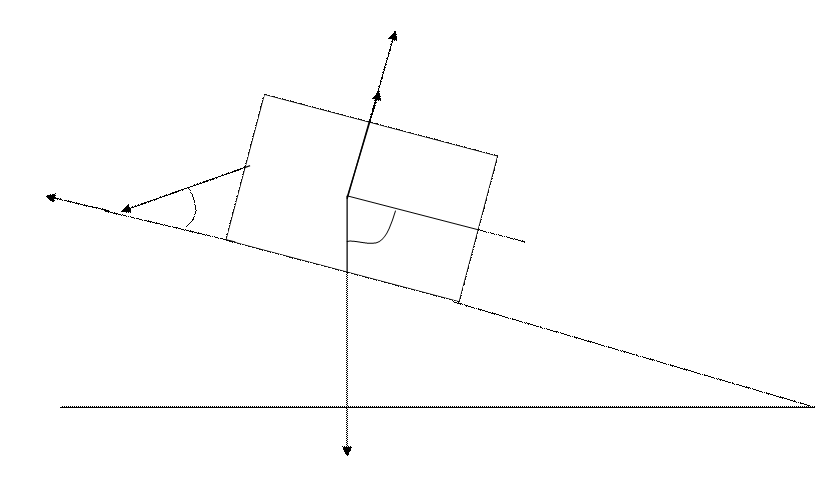
Y

N

T

F_тр                β                            

α

G₁

Рисунок 2.

Запишем 2 закон Ньютона:

OY: N-G₁*sinα-T*sinβ= 0

N= T* sinβ+ G₁*sinα

F_тр= f*N= f*(T* sinβ+ G₁*sinα)       

             β= arctg (l/σ)

            Таким образом, окончательно получаем выражение для нахождения силы трения колес изделия о пол самолета: