10 Расчет выправки железнодорожных кривых
Как бы идеально правильно ни была уложена в плане кривая, после прохождения определенного количества поездов ее геометрические очертания будут неизбежно нарушены или, как говорят, "кривая будет сбита". В первую очередь это относится к кривым с малыми радиусами, а также к кривым, имеющим непостоянный радиус. При этом кривые наиболее нарушены в условиях повышенных скоростей движения, слабых балластов и рельсошпальной решетки, когда путь недостаточно устойчив, а воздействие подвижного состава на него велико.
Работы по выправке кривых заключаются в отрихтовывании их в геометрически правильное положение, возможно и отличное от первоначального проектного, и связаны со специальным расчетом. Целью расчета является определение удовлетворяющих условиям задачи сдвигов, или рихтовок, в ряде точек кривой, необходимых для придания кривой правильного положения.
Под правильным положением кривой в плане следует понимать соблюдение плавности переходных кривых и постоянства радиуса кругового участка. Если кривая составлена из участков различных радиусов, должен быть обеспечен плавный переход от одного радиуса к другому.
Весь комплекс работ по выправке расстроенных кривых состоит из следующих основных этапов: съемки существующей натурной кривой, расчета рихтовок, или сдвигов, подготовки и производства самой рихтовки или постановки кривой в проектное положение.
Съемка кривой
Исходными материалами для расчета выправки кривой являются данные, полученные при съемке кривой. Процесс съемки заключается в измерении в определенных местах кривой так называемых стрел прогиба. Для этого вся кривая делится на равные участки длиной по 10 м при радиусе кривой R > 400 м или 5 м при R < 400 м.
Для замера стрел прогиба в каждой точке деления кривой две соседние с ней точки деления соединяются шнуром, являющимся хордой 20-метровой длины (так называемой хордой-двадцаткой). Затем в данной точке измеряется расстояние между рабочей гранью наружного рельса и шнуром-хордой. Это расстояние и есть стрела прогиба.
Замеры начинают и заканчивают на четко выраженных прямых, то есть в точках, где стрелы прогиба равны нулю. Для этого на каждом из смежных с кривой прямых участках дополнительно отмечаются не менее чем три - четыре точки деления (рисунок 21).
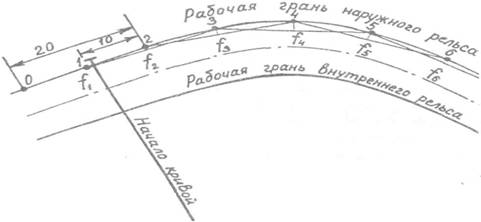
Рисунок 21 - Разбивка кривой
При измерении стрел прогиба измеряют также допустимые величины сдвижек пути в каждом направлении (справа, слева по ходу пикетажа) в зависимости от местных ограничивающих условий. Возможными препятствиями для сдвига являются искусственные сооружения: мосты, тоннели, трубы, стоящие вблизи здания, а также путевые знаки, недостаточная ширина обочины (менее 0,20 м) и т.д.
Существующие методы расчета выправки кривых
Существует значительное число различных способов расчета выправки кривых, снятых по стрелам изгиба, которые, в основном, сводятся к двум методам: методу разности эвольвент, и методу последовательных приближений. Оба этих метода используют основную зависимость проектных стрел от натурных стрел и сдвигов:
![]() , (10.1)
, (10.1)
где Fn - проектная стрела в точке n;
fn - натурная стрела в точке n;
en - сдвиг в точке n;
e n+1, e n-1 - сдвиги в смежных точках.
При методе разности э в о л ь в е н т сдвиг кривой в каждой точке рассматривается как разность эвольвент проектной и натурной кривых. Расчет сдвигов производится по формуле
![]() (10.2)
(10.2)
В методе разности эвольвент большое практическое значение имеет правильное определение проектных стрел. Неудачное назначение проектных стрел приводит к большим сдвигам, да и вообще этот метод сам по себе не обеспечивает минимума рихтовок. В этом методе установлен единственный порядок расчета, приводящий к тому, что определенным, принятым для расчета проектным стрелам будет соответствовать определенное, единственное значение сдвигов. Поэтому, чтобы уменьшить величины сдвигов или свести их к нулю в фиксированных точках, необходимо изменить принятые проектные стрелы. Для этого приходится применять различные расчетные приемы, использующие график суммы разности стрел (в графоаналитическом способе) и график суммы сумм разности стрел — график полусдвигов. В графоаналитических приемах по графику полусдвигов определяют сдвиги в каждой точке кривой или находят, в каких точках и на сколько нужно изменить проектные стрелы, чтобы сдвиги удовлетворяли поставленным требованиям, а затем вновь повторяют весь расчет.
Метод разности эвольвент следует применять, когда кривая не сильно сбита, т. е. когда сдвиги небольшие и по протяжению кривой меняются по знаку.
Метод последовательных приближений основан на геометрической зависимости стрелы изгиба в каждой точке кривой от сдвигов в соседних с ней точках. В этом методе сдвиги определяют путем постепенного приближения к принятым расчетным стрелам
![]() ,
(10.3)
,
(10.3)
где Fn — стрела, принятая в начале расчета;
Δen — дополнительный сдвиг,
получаемый после m-го приближения (обычно достаточно трех
приближений).
При этом принятые расчетчиком стрелы не обязательно точно совпадают со
стрелами проектной кривой.
При расчете кривых по методу последовательных приближений величины сдвигов получаются меньшими, чем при подсчете по методу разности эвольвент, однако стрелы после выправки кривой, расчитанной по методу последовательного приближения, не строго совпадают с проектными, но получаются в пределах допусков. Поэтому методом последовательного приближения следует пользоваться в основном при текущем содержании пути, когда нужно выправить кривую относительно проектного положения, уже заданного паспортом кривой. При этом, однако, необходимо помнить, что многократное применение этого метода может привести к потере проектного положения кривой. Для постановки кривой в проектное положение следует применять метод разности эвольвент.
На методе последовательных приближений основан и самый простой способ расчета выправки кривых, использующий принцип, непосредственно заложенный в формуле (10.1): при сдвиге пути в какой-либо точке n стрела в этой точке изменится на величину сдвижки, а в соседних точках n—1 и п+1, расположенных по обе стороны от нее и остающихся неподвижными, стрелы изменяются на половину величины сдвижки в точке п с обратным знаком за счет изменения положения хорд (рисунок 22).
В результате при сдвиге пути в точке п на величину еп стрелы в точке п и смежных с ней будут равны:
![]()
![]()
![]()
В соответствии с этим принципом производится постепенное смягчение нарушений графика стрел регулировочным способом.
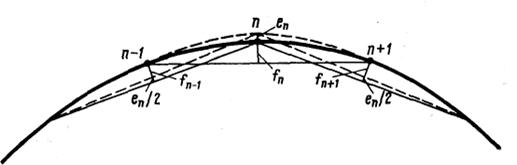
Рисунок 22 - Схема изменения положения хорд и стрел изгиба при сдвиге в точке п
Графоаналитический способ расчета выправки кривых
Расчет выправки производится в следующем порядке:
Задаются проектными стрелами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.