Оценка движения основных фондов. Движение основных производственных фондов за год. Продолжительность действия (бездействия) основных производственных фондов за год, страница 7

6. Подставляя F(x)  в выражение (*), будем иметь:

= .

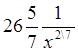7. Разрешая последнее уравнение относительно х, найдём функцию спроса            

х_с =27603,1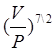

8. Обозначим значение   функций спроса  при 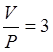 через х₀, тогда х₀ = 1290869.

9.  Подставляя х_с  в производственную функцию, найдём функцию предложения:

У_п = 38642,1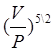

10. При 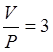  функция предложения будет иметь значение 

Уо = 602370,7.

Задача 11.9 Использование метода Лагранжа для

            определения максимальной еженедельной

             прибыли и соответствующего спроса.

При изготовлении холодильников завод использует голландские и финские компрессоры. Установка каждого голландского компрессора даёт заводу 5 грн., а финского — 6 грн. Согласно условиям поставок каждую неделю завод может устанавливать х и у (тыс.) голландских и финских компрессоров соответственно, причём х и у связаны условием:

φ(х,у) = х² + у² + 2х + 4у – 56 + 0;

Найти с помощью метода Лагранжа максимальную еженедельную прибыль и соответствующий спрос на количество голландских и финских компрессоров.

Решение.

1.     Необходимо     найти     максимум    функции

П(х,у) = 5х + 6у при условии, что уравнением связи являются:

φ(х,у) = х² + у² + 2х = 4у – 56 = 0;

2. Составим функцию Лагранжа:

Ф(х, у, λ) = f(x, у) + λ φ(х, у)= х + 6у + λ(х² + у² + 2х + 4у –56) Необходимое условие экстремума этой функции:

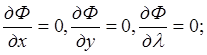
Отсюда получаем систему трёх уравнений относительно трёх неизвестных х, у, λ:

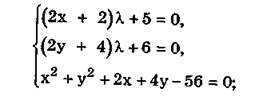
3.  Эта система имеет решения:

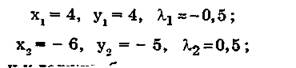
Так как х и у должны быть неотрицательными, то решение (х₂, у₂, λ₂ ) учитывать не будем.

Таким образом, имеем одну критическую точку M₁ (4; 4; – 0,5) функции Лагранжа.

4.  Проверим эту точку на относительный экстремум с помощью достаточных условий.   Для этого найдём вторые частные производные:

Р=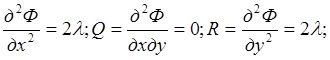

Тогда в точке М₁ (4;;4-0,5)   Р= –1;  Q=0;   R = –2.

В этом случае  РR – Q² = 2 > 0,  P < 0, значений, точка (4,4) является точкой строго относительно максимума.

5. Для нахождения максимальной еженедельной прибыли подставим х₁ =4 в функцию:

П(х,у) = 5х + 6у, т.е. П_max = П(4,4) = 5·4 + 6·4 = 44 тыс.грн.

6. Спрос на компрессоры будет: х = 4 (тыс.ед.) и  у = 4 (тыс.ед.).

Задача 11.10. Установление эмпирической зависимости показателей фондоотдачи и

удельного веса активных производственных фондов.

В таблице приведены данные о фондоотдаче и удельном весе активных элементов основных производственных фондов на производственном объединении на 2006 -2010 годы.

Годы	2006	2007	2008	2009	2010
Xi	32,2	42,3	27,4	37,1	32,4
Уi	1,2	1,3	1,1	1,9	1,3

Здесь х_i — удельный вес машин и оборудования в основных производственных фондах в процентах; y_i — фондоотдача в гривнах.

Вывести эмпирическую формулу зависимости фондоотдачи от удельного веса активных элементов основных производственных фондов, считая эту зависимость линейной.

Решение.

1.  По условию задачи связь между х и у линейна, то есть:

y = f (x) = ax + b.

Нам необходимо по имеющимся данным найти  параметры а и b. Задача сводится к отысканию таких значений  а и b, при которых функция:

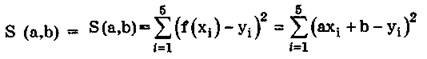
принимает наименьшее значение.

2.  Для нахождения   а и b решим систему:

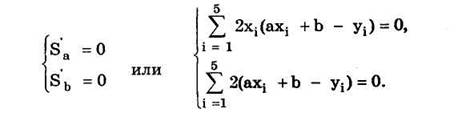
3. После некоторых преобразований система примет вид:

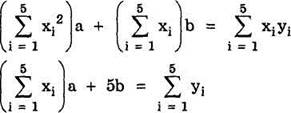
4.  С целью получения коэффициентов при а и b и свободных членов системы составим  вспомогательную таблицу:

I	xi	yi	xi yi	xi2
	32,2 42,3 27,4 37,1 32,4	1,2 1,3 1,1 1,9 1,3	38,64 54,99 30,14 70,49 42,12	1036,84 1789.29 750,76 1376,41 1049,76
	171,4	6,8	236,38	6003,06

5. Используя данные таблицы, получим окончательно систему:

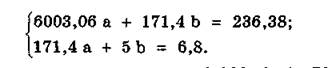
Эта системаимеет решение а = 0,026, b = 0,479

6.  Таким образом, эмпирическая формула зависимости фондоотдачи от удельного веса активных элементов основных производственныхфондов имеет вид: