Оценка движения основных фондов. Движение основных производственных фондов за год. Продолжительность действия (бездействия) основных производственных фондов за год, страница 6

5. Определяем абсолютное изменение балансовой прибыли, планируемой по сравнению с отчетной (∆П_бал ):

∆П_бал =1064,66 – 549 = 515,66 тыс. грн.

6. Определяем относительное изменение балансовой прибыли планируемой по сравнению с отчетной (∆П_{бал %})

∆П_{бал %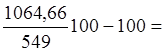} =93,9%.

Задача 9.1  ПРИВАТИЗАЦИЯ ПРЕДПРЯТИЙ

АО выпустило 900 простых акций и 100 привилегированных, а также 150 облигаций. Номинальная стоимость всех ценных бумаг — 100 000 грн. Процент по облигациям — 12%. Дивиденд по привилегированным акциям — 15%.

Определить дивиденд от прибыли. Расположить всех держателей ценных бумаг по стадиям доходности, если прибыль по распределению составила 16000 тыс. грн.

Решение.

1. Определяем дивиденды от прибыли (Д):

Д=Сд Нст, где:   Сд — ставка дивиденда по акциям (облигациям), %;

Нст — номинальная стоимость ценных бумаг, грн.

По привилегированным акциям:

Дпр = 0,15 х 100000 = 15000 грн.

По обыкновенным акциям:

Д_об = 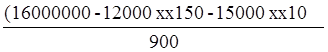=14 111 грн.

По облигациям:

Д_обл = 0,12 х 100000 = 12000 тыс. грн.

2. Расположим всех держателей ценных бумаг по стадиям доходности:

Привилегированная акция — 15 000 грн.

Обыкновенная акция — 14 111 грн.

Облигация — 12 000 грн.

Задача 11.6.   Выбор политики фирмы на основе

                              максимизации прибыли.

Фирма стремится осваивать два различных рынка.

Пусть цены Pi (i=l,2) выражаются формулами:

P1=360 – q₁,    P2 =140 – 2q₂ , т.е линейно падают с увеличением объёма предъявления готовой продукции. q₁( i = l,2). Суммарная функция издержек имеет вид:

C(q) = 3600 + 2q.

Здесь слагаемое 3600 представляет постоянные затраты, а слагаемое 2q — переменные затраты, причём q = q1 + q2.

Какую ценовую политику должна проводить фирма, чтобы  прибыль была максимальна?

Решение.

1. Для решения находим предельные издержки, одинаковые для обоих рынков:

Cq=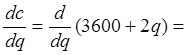2.

2.  Суммарный доход для первого рынка   вычисляем как:

R₁ =P₁q₁ =(360– q₁)q₁ = 360q₁ –q²₁

3. Предельный доход для первого рынка:

R₁q₁=,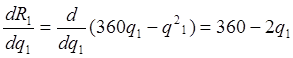

4. Так как в критических точках R₁q_{1 =} C_q , то подставляя полученные выражения, находим:

360 – 2q₁ =2 => q₁ = 179.

5. Подставляя q₁ в формулу определения спроса первого рынка получим:

P₁ = 360 – 179 = 181 (ден.ед.).

6. По аналогии получим суммарный и предельный доходы для второго рынка:

R₂ = P₂ q₂ = (140 – 2q₂ )q₂ = 140q₂ – 2q² ₂ ,

R₂ q₂ 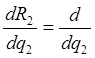 =(140q₂ – 2q_l²) = 140 – 4q.

7. Приравнивая последнее выражение к предельным издержкам, получим:

140 - 4q₂ = 2, откуда находим

q₂ = 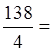34,5

8. Соответствующая цена находится из кривой спроса второго рынка:

Р₂  = 140 – 2 x 34,5 = 140 – 69 = 71 (ден. ед.).

Вывод. Для получения максимальной прибыли фирме следует продавать товар на первом рынке по цене

P₁ =181 (ден.ед.), а   на втором   по цене  Р₂ =71 (ден.ед.).

Задача 11.7. Определение предельных и частных

                         значений фондоотдачи, функций спроса и

                          предложения.

Пусть фирма, выпускающая один товар, характеризуется своей производственной функцией

F(x) = 26x^{5 / 7} , т.е. зависимостью объёма выпуска продукции у от объёма основных фондов х . В настоящий момент объём основных фондов  в  равен  b =128.

1. Найти среднюю и предельную фондоотдачи, эластичность выпуска по фондам. Решить задачу фирмы, т. е. найти объём  перерабатываемого ресурса, при котором выпуск продукции дает максимальную прибыль.

2. Найти функцию спроса на ресурсы и функцию предложения продукции.

3.  Найти частные   значения   этих функций полагая, что   цена единицы   продукции   в три раза больше цены единицы ресурса.

Решение.

1. Средняя фондоотдача f равна:

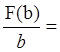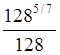f=26= 6,5

2. Предельная фондоотдача:

F'(b) = .

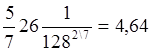3. Эластичность выпуска по фондам равна:

F'(b)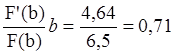

4.  Решаем задачу фирмы. Пусть Р — цена единицы ресурса, а V — единицы выпускаемого товара. Следовательно, прибыль фирмы определяется по формуле:

П(х) = V F(x) – P x

5.  Приравнивая производную функции П(х) к нулю получим:

П'(x)= VF'(x) – P = 0 =>F'(x) =

Так как объем перерабатываемого ресурса положителен, то  точка х определяемая соотношением будет внутренней, т.е. точкой экстремума.

Поскольку   F"(x) = 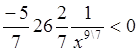 , то это будет точка максимума. Значение хс, определяемое соотношением (*) называется оптимальным и оно единственное для данного отношения .