Расчет и конструирование центрально-растянутых элементов. Несущаяспособность растянутого элемента, страница 7

Определяем опасное сечение в балке находящееся на расстоянии «Х» от опоры по формуле:

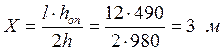
где: h_оп= 490 м – высота балки на опоре (принята конструктивно, но  не менее h/2).

Определяем изгибающий момент в сечении «Х» по формуле:

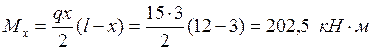
Определяем высоту балки в сечении «Х» определяем по формуле:

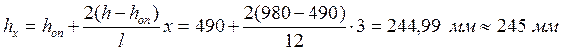
Определяем момент сопротивления балки в сечении «Х» по формуле:

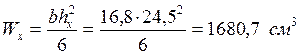
Проверяем прочность балки по формулам:

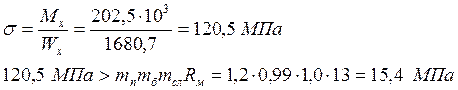
где: т_п, т_б, т_сл – коэффициенты приняты по табл. 7П, 10П, 11П приложения.

Прочность по нормальным напряжениям не обеспечена.

Для обеспечения прочности балки вновь подбираем (варианты) сечения до полного соответствия требований, установленных нормативами и дополнительно, конструктивно обеспечиваем прочность и устойчивость балки (через установку связей каркаса здания).

Проверяем прочность балки на действие касательных напряжений.

Определяем максимальную поперечную силу по формуле:

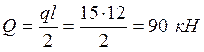
Далее определяем момент инерции и статической площади для опорного сечения (где действует Q_max) по формулам имеем:

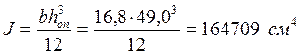
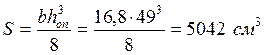
Проводим проверку прочности балки по формуле касательных напряжений.

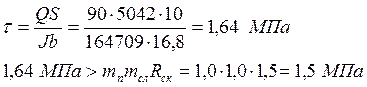
Прочность балки не обеспечена.

Для проверки устойчивости определяем коэффициент φ_м по формуле (3.11) [11]. При отсутствии связей по верхним поясам балок при l_p = 12 м, тогда по формуле определяем:

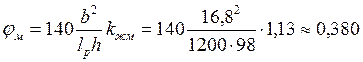
где: k_ф = 1,13 см. табл. 25П приложения.

Поскольку балка переменной высоты сечения и не имеет закреплений из плоскости по растянутой от момента «М» кромке, коэффициент φ_м необходимо умножить на дополнительный коэффициент k_жм. Для данного случая коэффициент k_ж.м = β^2/5= 0,8 (см. табл. 25П приложения).

где: β = h_on/h = 49/94,5 = 0,5.

Определяем момент сопротивления сечения в середине пролета балки по формуле:

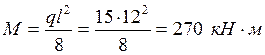
Определяем момент сопротивления сечения в середине пролета балки по формуле:

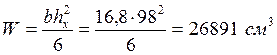
Проверяем устойчивость  балки по формуле:

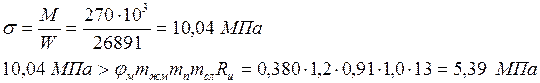
Устойчивость балки при отсутствии связей не обеспечена. Необходимо устанавливать связи. Ставим связи с шагом 3,3 м, тогда l_p= 3300 мм, коэффициент φ_м· k_ж.м будет равен 1,255 · 0,8 = 1,004 > 1 и условие устойчивости будет выполнено.

Проверяем прогиб балки по формуле (9.5) [11]

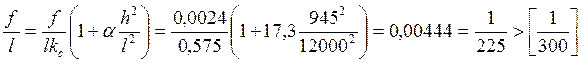
где: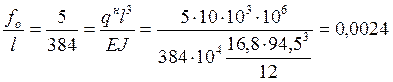        

 (см.табл. 26П приложения), учитывается переменная высота сечения балки;

 (см. табл. 26П приложения), учитывает влияние поперечных сил.

Жесткость балки недостаточна.

Для обеспечения жесткости балки выполняем работы и конструктивные решения, указанные  в расчетах выше (см. вариант II б).

Расчет и конструирование трапециевидных, сегментных, брусчатых ферм

Практикум

2 часа

Пример 11.

Проверить прочность первой (от опоры) панели верхнего пояса фермы (см. рис.), загруженного равномерно распределенной вертикальной нагрузкой «q»по всему пролету.

Материал пояса принят из сосны 2-го сорта, коэффициенты т_б,  т_сл для случая клееного пояса принимаем равным 1,0.

Рис. 11. К расчету верхнего пояса предельной фермы

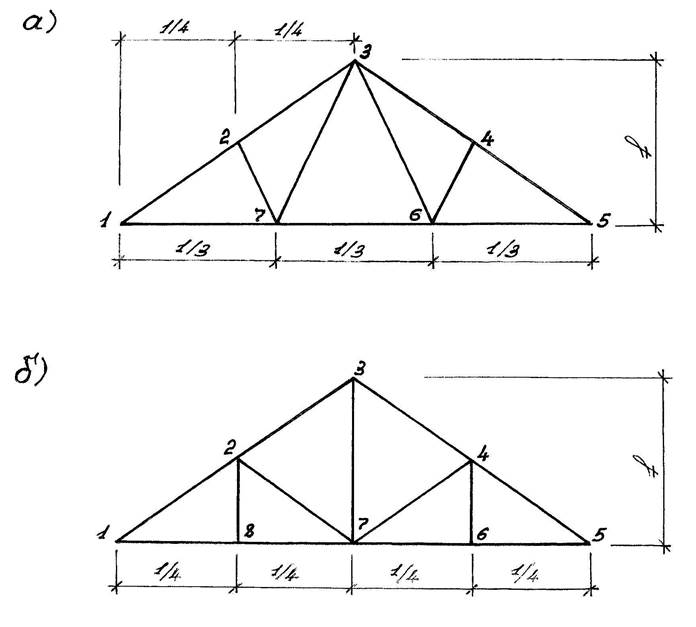
Вариант II, схема «а».

Исходные данные принимаем из табл. 7.

Таблица 7

№ п/п	Исходные данные
	А					Б
	Схема фермы по рис.	Эксцентриситет в узлах	Пролет фермы, мм	Разредность верхнего пояса	Усилие в элементе от единичной узловой нагрузки	Распределенная нагрузка, кН\м	Длина элемента, мм	Сечение элемента
								b, мм	h, мм
1	а	0,15h	12000	неразрезной	4,04	10,0	3230	150	200
2	б	0,2h	13000	разрезной	4,04	12	3230	200	200

Решение.

Для расчета проводим уточнение исходных данных:  принято для сосны 2-го сорта.

Определяем площадь сечения элемента:

Рассчитываем момент сопротивления:

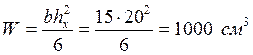
где: l_o = 3230 мм – расчетная длина элемента фермы (см. табл. 7).

Определяем гибкость элемента фермы:

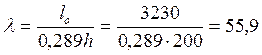
Определяем узловую нагрузку на ферму по формуле: