Далее определяем момент инерции и статической площади для опорного сечения (где действует Qmax) по формуле имеем:
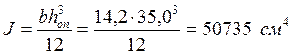
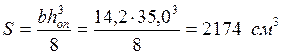
Проводим проверку прочности балки по формуле касательных напряжений:
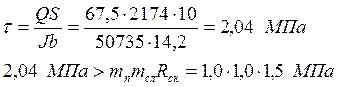
Прочность балки по касательным напряжениям не обеспечена.
Для проверки устойчивости определим коэффициент φм по формуле (3.11) [13]. При отсутствии связей по верхним полкам балок lp= 9 м, тогда
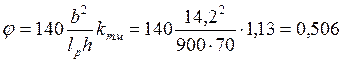
где: kф=1,13 см. табл. 25П приложения.
Поскольку балка переменной высоты сечения и не имеет закреплений из плоскости по растянутой от момента «М» кромке, коэффициент φм необходимо умножить на дополнительный коэффициент kж.м. Для данного случая коэффициент kж.м = β2/5= 0,8 (см. табл. 25П приложения), где: β = hon/h = 350/700 = 0,5.
Определяем изгибающий момент в середине пролета по формуле:
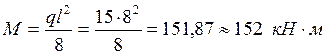
Определяем момент сопротивления сечения в середине пролета балки по формуле:
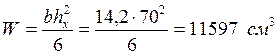
Проверяем устойчивость балки по формуле:
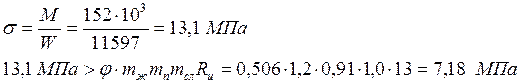
Устойчивость балок при отсутствии связей не обеспечена. Необходимо установить связи. Ставим связи с шагом 3,3 м, тогда lp= 3300 мм, коэффициент φм· kж.м будет равен 1,255 · 0,8 = 1,004 > 1,0 и условие устойчивости будет выполнено.
Производим проверку прогиба балки по формуле:
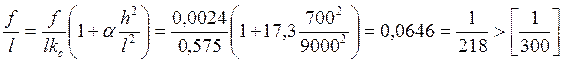
где: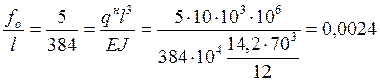 
(см.табл.
26П приложения), учитывает переменную высоту сечения балки).
(см.
табл. 26П приложения), учитывает влияние поперечных сил.
Жесткость балки недостаточна.
Для обеспечения жесткости балки дополнительно принимаем конструктивное решение при монтаже каркаса здания.
Вариант II (б).
Для расчета принимаем исходные данные из табл. 6 рис.10.
Определяем опасное сечение в балке находящееся на расстоянии «Х» от опоры по формуле:
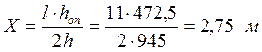
где: hоп= 472,5 м – высота балки на опоре (принята конструктивно не менее h/2).
Определяем изгибающий момент в сечениях «Х» по формуле:
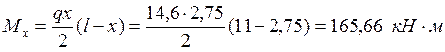
Высоту балки в сечении «Х» определяем по формуле:
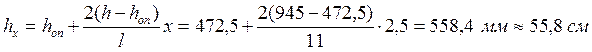
Определяем момент сопротивления балки в сечении «Х» по формуле:
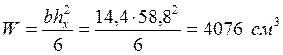
Проверяем прочность балки по формуле:
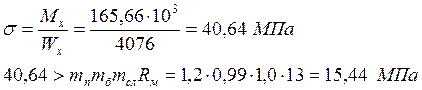
где: тп, тб, тсл – коэффициенты приняты по табл. 7П, 10П, 11П приложения.
Прочность по нормальным напряжениям не обеспечена. Для обеспечения прочности балки вновь подбираем варианты сечения до полного решения в соответствии требований, установленных нормативами и дополнительно, конструктивно обеспечиваем прочность и устойчивость балки (через установку связей каркаса здания).
Проверяем прочность балки на действие касательных напряжений.
Определяем максимальную поперечную силу по формуле:
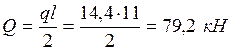
Далее определяем момент инерции и статической площади (где действует Qmax) по формулам:
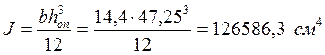
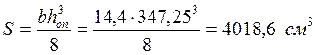
Проводим проверку прочности балки по формуле касательных напряжений.
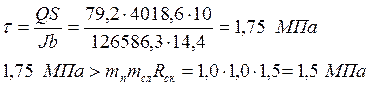
Прочность балки не обеспечена. Для проверки устойчивости определяем коэффициент φм по формуле (3.11) [11]. При отсутствии связей по верхним поясам балок при lp = 11 м, тогда по формуле определяем:
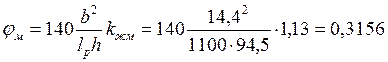
где: kф = 1,13 см. табл. 25П приложения.
Поскольку балка переменной высоты сечения и не имеет закреплений из плоскости по растянутой от момента «М» кромке, коэффициент φм необходимо умножить на дополнительный коэффициент kжм. Для данного случая коэффициент kж.м = β2/5= 0,8 (см. табл. 25П приложения).
где: β = hon/h = 472,5/945 = 0,5.
Определяем момент в середине пролета балки по формуле:
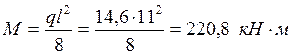
Определяем момент сопротивления сечения в середине пролета балки по формуле:
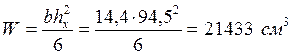
Проверяем прочность балки по формуле:
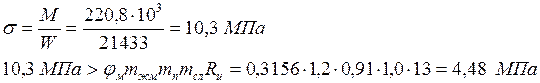
Устойчивость балки при отсутствии связей не обеспечена. Необходимо устанавливать связи. Ставим связи с шагом 3,3 м, тогда lp= 3300 мм, коэффициент φм· kж.м будет равен 1,255 · 0,8 = 1,004 > 1 и условие устойчивости будет выполнено.
Проверяем прогиб балки по формуле (9.5) [11]
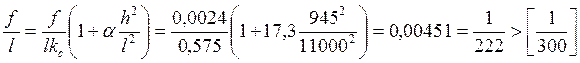
где: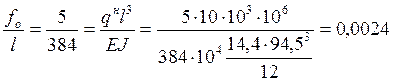 
(см.табл.
26П приложения), учитывается переменная высота сечения балки;
(см.
табл. 26П приложения), учитывает влияние поперечных сил.
Жесткость балки недостаточна.
Для обеспечения жесткости балки выполняем мероприятия, указанные в расчетах выше (см. вариант II б)
Вариант III (в).
Для расчета принимаем исходные данные из табл. 6 и рис. 10.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.