Расчет и конструирование центрально-сжатых элементов конструкций
Практикум
2 часа
Пример 3.
Найти несущую способность центрально-сжатого стержня (см. рис. 3).
Рис. 3. К расчету центрально-сжатого стержня
Исходные данные принимаем по таблице 3.
Таблица 3
|
№ п/п |
Исходные данные |
||||||||
|
А |
Б |
||||||||
|
l, мм |
h, мм |
b, мм |
D, мм |
Схема закрепления концов в плоскости |
Материал |
Условие эксплуатации |
Сорт |
||
|
х - х |
у - у |
||||||||
|
1 |
3000 |
200 |
150 |
40 |
ш - ш |
ш - ш |
Пихта |
А3 |
2 |
|
2 |
6000 |
250 |
150 |
28 |
3 – 0 |
ш - ш |
Кедр |
Б3 |
1 |
|
3 |
4000 |
225 |
175 |
20 |
3 - ш |
ш - ш |
Граб |
В3 |
2 |
Вариант I.
Решение
Определяем несущую способность центрально-сжатого стержня с учетом его устойчивости по формуле:
![]()
где: тп = 0,8 – коэффициент перехода на породу дерева (см. табл. 7П приложения);
тв = 0,9 – коэффициент, учитывающий условия эксплуатации конструкции или группы конструкций (см. табл. 8П приложения);
Rс = 13 МПа – расчетное сопротивление древесины, для сосны второго сорта (см. табл. 6П приложения).
Поскольку сечение ослаблено отверстием Ø 40 мм, то определяем площадь ослабления по формуле:
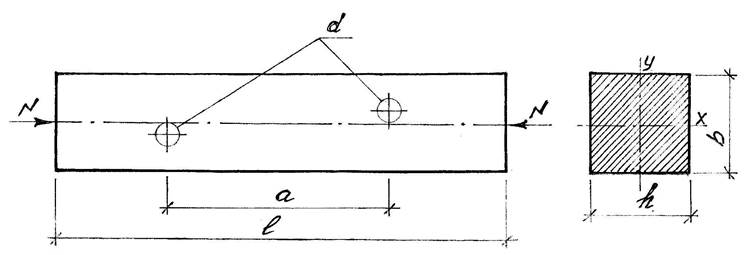
![]() , что в процентном отношении составит:
, что в процентном отношении составит:
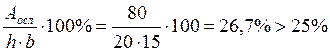
Рассчитываем площадь сечения для проверки устойчивости стержня по формуле:
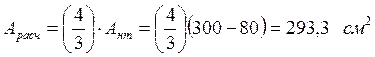
Определяем коэффициент φ через гибкость элемента по формуле:
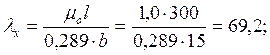
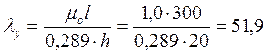
Расчет ведем по наибольшему значению λх= 69,2.
При условии, что для гибкости λ < 70, определяем коэффициент φ по формуле:
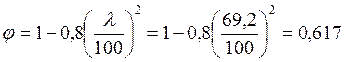
Определяем несущую способность стержня по формуле:
![]()
Вариант II.
Расчет ведем аналогично по тем же формулам, при тех же условиях работы стержня (исходные данные принимаем по табл.3).
![]()
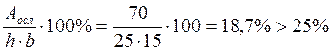
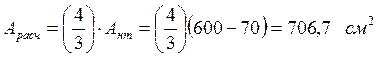
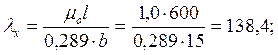
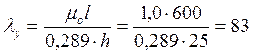
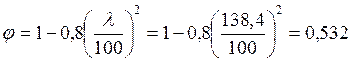
![]()
Вариант III.
Расчет ведем аналогично выше указанному решению и аналогичным описаниям.
![]()
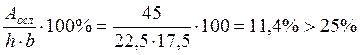
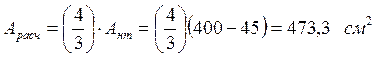
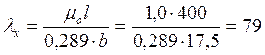
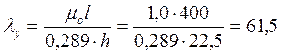
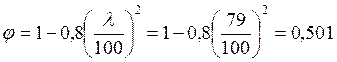
![]()
Анализ расчета и конструирования (по вариантно) показывает, что несущая способность центрально сжатых стержней прямо зависит от принятого сечения, сорта, вида древесины и схемы закрепления (расчетной схемы).
Расчет и конструирование изгибаемых элементов
и сжато-изгибаемых элементов конструкций
Практикум
2 часа
Пример 4.
Проверить устойчивость сжато-изогнутого элемента прямоугольного сечения, не раскрепленного из плоскости (см. рис.).
Рис.4. К расчету сжато-изогнутого элемента
Схема А Схема Б
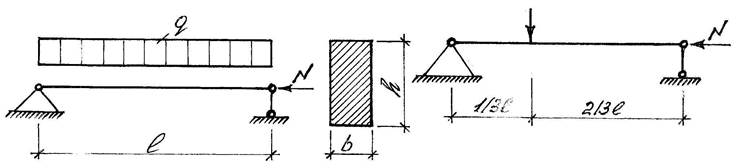
Для расчета исходные данные принимаем по таблице 4.
Таблица 4
|
№ п/п |
Исходные данные |
||||||
|
А |
Б |
||||||
|
Схема элемента |
N, кН |
q, кН/м |
l, мм |
b, мм |
h, мм |
Материал, сорт |
|
|
1 |
А |
20 |
4 |
2000 |
50 |
200 |
Лиственница, 2 с. |
|
2 |
Б |
45 |
5 |
3000 |
60 |
200 |
Ель, 1 с. |
|
3 |
А |
60 |
6 |
4000 |
60 |
250 |
Клен, 2 с. |
Решение.
Вариант I.
Проверку устойчивости стержня из плоскости выполняем по формуле, но для чего сначала найдем величину
![]()
![]()
где: тп = 1,2 – коэффициент, применяемый для лиственных пород древесины.
Определяем гибкость стержня и значения коэффициента φ:
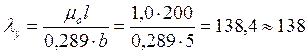
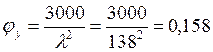
Проверяем устойчивость стержня:
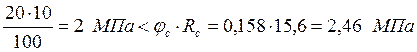
Устойчивость стержня их плоскости обеспечена.
Проверяем устойчивость плоской формы деформирования от совместного действия N и M по формуле, но для точного расчета предварительно определим требуемые величины:
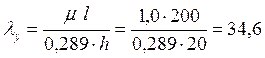
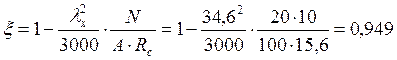
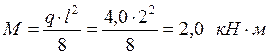
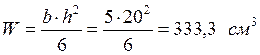
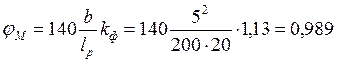
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.