Многочлены
Различают одночлены: 6, 3х, 5q2m многочлены: 6 – x, 3x – 2y, 5x2 + 24x + 3 (мономы и полиномы соответственно). Нулем многочлена p называется корень p(x) = 0. 1.Утверждение о нулях многочлена: Теорема Виета. А. Для квадратного трехчлена: p(x) = ax2 + bx + c В. Для кубического многочлена: p(x) = ax3 + bx2 + cx + d С. Для многочлена степени n: p(x) = a0xn + a1xn–1 + … + an
2. Утверждение о целых корнях многочлена с целыми коэффициентами. Если ищутся нули многочлена с дробными коэффициентами, они являются нулями многочлена с целыми коэффициентами. Целые корни многочлена (если есть) являются делителями его свободного члена.
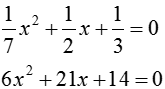
3. Утверждение о дробных корнях многочлена: Они ищутся среди дробей Докажем утверждение на примере: Пусть p(x) = x2 – 3x – 12. Число 5 не может быть корнем этого многочлена, поскольку если подставить 5, левая часть уравнения будет представлять собой число кратное 5 и уменьшенное на 12, что не дает нуля. Аналогично 10, при подстановке даст число кратное 10 и уменьшенное на 12 и т. д. Вообще для числа n мы будем иметь число кратное n, уменьшенное (увеличенное) на свободный член. Для того, чтобы получался ноль, n должно быть делителем свободного числа.
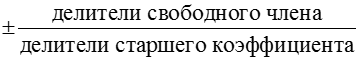
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.