Дифференциальные уравнения первого порядка. Общие решения дифференциального уравнения. Задачи, приводящие к дифференциальным уравнениям

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

При решении многих, прежде всего физических, задач встречаются уравнения, в которых неизвестной является некоторая функция. Если в уравнение входят производные искомой функции, то они называют дифференциальными уравнениями.

Например, уравнения

                                                    являются дифференциальными уравнениями, так как в них надо найти функцию  и в этих уравнениях содержатся производные этой функции.

Если в дифференциальное уравнение входит только производная первого порядка, то такое уравнение называют дифференциальным уравнением первого порядка.Если в дифференциальное уравнение входит производная второго порядка и не входят производные порядка выше второго, то такое уравнение называют дифференциальным уравнением второго порядкаи т. д. Поэтому дифференциальное уравнение (1) — первого порядка, а дифференциальное уравнение (2) — второго порядка.

Решением дифференциального уравненияназывают любую функции , при подстановке которой в дифференциальное уравнение получается тождество.

Например, функция есть решение дифференциального уравнения

Действительно,

Отметим, что любая функция вида

                                                     где  — любое число, также является решением дифференциального уравнения (3), так как .

Функцию (4) называют общим решением дифференциального уравнения(3). Давая  какие-либо значения, будем получать частные решения дифференциального уравнения(3).

Так, функции   (при , , , соответственно) являются частными решениями дифференциального уравнения (3).

Простейшее дифференциальное уравнение первого порядка имеет вид

                                                      где  — непрерывная на всей оси элементарная функция. Мы видим, что искомое решение уравнения (5) есть любая первообразная от функции , т. е. неопределенный интеграл

Здесь к некоторой первообразной от функции  прибавляется произвольная постоянная .

В рассмотренном выше примере  и поэтому по формуле (6) общее решение дифференциального уравнения (3) действительно выражается формулой (4).

Формула (6) выражает общее решение дифференциального уравнения (5), отдельные частные решения уравнения (5) получаются, если константе  придавать различные значения, а других решений нет.

Если дано дифференциальное уравнение , то его общее решение всегда можно найти так, как показано в следующем примере.

Пример. Найдем общее решение уравнения

Обозначим , тогда уравнение (7) можно переписать в виде . Его решение есть функция , где  — произвольная константа.

Так как функция , то получаем уравнение . Его решение, а значит и решение уравнения (7), есть функция

                                 где  — произвольная константа.

Итак, общее решение уравнения (7) есть функция

где и — любые константы, которые можно задавать независимо друг от друга.

Давая  и  какие-либо значения, будем получать частные решения уравнения (7). Например, функции  являются частными решениями уравнения (7).

Задачи, приводящие к дифференциальным уравнениям

1. Задача о нахождении пути по заданной скорости. Пусть точка движется со скоростью . Нужно найти путь , пройденный точкой от момента  до момента . Обозначим  путь, пройденный точкой за время . Тогда , т. е.  — первообразная для функции . Поэтому по формуле Ньютона — Лейбница 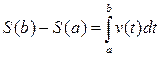. Так как , то искомый путь равен

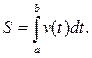
Например, если точка движется со скоростью  (м/с), то путь, пройденный точкой за первые 10 с, по формуле (1) равен

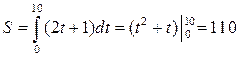 (м).

2. Задача о вычислении работы переменной силы. Пусть тело, рассматриваемое как материальная точка, движется по оси под действием силы , направленной вдоль оси . Вычислим работу силы при перемещении тела из точки  в точку .

Пусть  — работа данной силы при перемещении тела из точки  в точку . При малом  силу на отрезке можно считать постоянной и равной . Поэтому , т. е.

Устремляя  к нулю, получаем, что , т. е. — первообразная для функции . По формуле Ньютона — Лейбница получаем 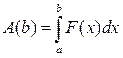, так как .

Итак, работа силы  при перемещении тела из точки  в точку равна

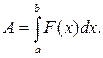
Заметим, что если  выражается в ньютонах (Н), а путь — в метрах, то работа  — в джоулях (Дж).

Пример. Вычислить работу силы при сжатии пружины на  м, если для ее сжатия